
分析 采用形数结合的方法解题,根据抛物线的开口方向,对称轴的位置判断a、b、c的符号,把两根关系与抛物线与x的交点情况结合起来分析问题.
解答 解:①由二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),
4a-2b+c=0,故①正确;
②因为图象与x轴两交点为(-2,0),(x1,0),且1<x1<2,
对称轴x=$\frac{-2+{x}_{1}}{2}$=-$\frac{b}{2a}$,
则对称轴-$\frac{1}{2}$<-$\frac{b}{2a}$<0,且a<0,
∴a<b<0,
由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,即a<b<c,故②正确;
③设x2=-2,则x1x2=$\frac{c}{a}$,而1<x1<2,
∴-4<x1x2<-2,∴-4<$\frac{c}{a}$<-2,
∴2a+c>0,4a+c<0,故③正确;
④c<2,4a-2b+c=0,
4a-2b+2>0,2a-b+1>0,故④错误;
故答案为:①②③.
点评 本题考查了抛物线图象与系数的关系,其中a由抛物线的开口方向决定,a与b同号对称轴在y轴左边;a与b异号对称轴在y轴右边,c的符合由抛物线与y轴的交点在正半轴或负半轴有关,利用了根与系数的关系,点与图象的关系,题目稍有难度.


科目:初中数学 来源: 题型:解答题
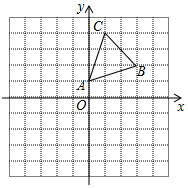 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
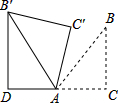 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=4,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=4,则AD的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
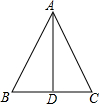 如图,AD⊥BC,D为BC的中点,有结论①△ABD≌△ACD,②∠B=∠C,③AD平分∠BAC,④△ABC是等边三角形,其中正确的有( )个.
如图,AD⊥BC,D为BC的中点,有结论①△ABD≌△ACD,②∠B=∠C,③AD平分∠BAC,④△ABC是等边三角形,其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com