
【题目】如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km的P地出发,向C站匀速行驶,15min后离A站30km.
(1)设出发x h后,汽车离A站y km,写出y与x之间的函数表达式;
(2)当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站.汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?
![]()
科目:初中数学 来源: 题型:
【题目】中学生上网现象越来越受到社会的关注,小记者小慧随机调查了某校若干学生和家长对上网现象的看法制作了如下的统计图1和2.请根据相关信息,解答或补全下列问题.

(1)补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)该校共有1600名学生,请你估计这所中学的所有学生中,对上网持“反对”态度的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例1:在等腰三角形ABC,∠A=120°,求B的度数.
例2:在等腰三角形ABC中,∠A=50°,求∠B的度数.
王老师启发同学们进行变式,小兰编了如下一题:变式等腰三角形ABC中,∠A=70°,求∠B的度数;
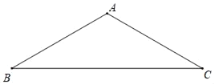
(1)请你解答小兰的变式题;
(2)解完(1)后,小兰发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°;
①当∠B的度数唯一时请你探索x的取值范围并用含x的式子表示∠B的度数;
②当∠B有三个不同的度数时请你探索x的取值范围,并用含x的式子表示∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个底边相等的等腰三角形按照图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是 ( )
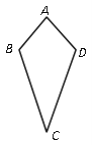
A. 有两组邻边相等的四边形称为“筝形”;
B. 有两组对角分别相等的四边形称为“筝形”;
C. 两条对角线互相垂直的四边形称为“筝形”;
D. 以一条对角线所在直线为对称轴的四边形称为“筝形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作二次函数表达式y=a(x﹣2)2+c中的a,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作表达式中的c.
(1)求抽出a使抛物线开口向上的概率;
(2)求抛物线y=a(x﹣2)2+c的顶点在第四象限的概率.(用树状图或列表法求解)
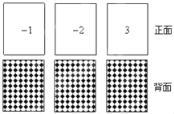
查看答案和解析>>
科目:初中数学 来源: 题型:
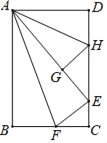
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O1与⊙O2相交于A、B两点,经过点A的直线CD分别与⊙O1、⊙O2交于C、D,经过点B的直线EF分别与⊙O1、⊙O2交于E、F,且EF∥O1O2.下列结论:①CE∥DF;②∠D=∠F;③EF=2O1O2.必定成立的有( )
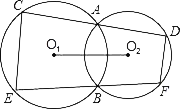
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
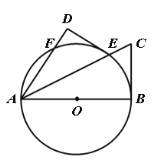
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com