练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．指出下列命题的条件和结论．
    （1）如果两个角相等，那么它们是对顶角；
    （2）若a＞b，b＞c，则a＞c；
    （3）全等的两个三角形的面积相等．

    分析 根据一个命题由题设和结论两部分组成，以如果开始的部分是条件，以那么开始的部分是结论，分别对（1）（2）（3）进行解答即可．

    解答 解：（1）如果两个角相等，那么它们是对顶角”的条件是：两个角相等，结论是：它们是对顶角；
    （2）若a＞b，b＞c，则a＞c的条件是a＞b，b＞c，结论是a＞c；
    （3）全等的两个三角形的面积相等的条件是两个三角形全等，结论是它们的面积相等．

    点评 本题主要考查了命题的组成，命题由题设和结论两部分组成．其中题设是已知的条件，结论是由题设推出的结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．（$\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$）÷（-$\frac{1}{36}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

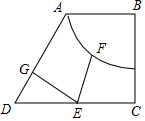    1．如图，直角梯形ABCD中，AB∥DC，∠B=90°，AB=1，BC=2，CD=3，以B为圆心，半径为1的弧交BC于M，E是线段CD上一动点，EG⊥AD，垂足为G，F是弧AM上一动点，则EG+EF的最小值为$\frac{5\sqrt{2}-2}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知二次函数y=ax2+k的图象经过点（-1，2），（0，-4），求该函数的解析式．并指出在对称轴左侧部分，y随x的增大将发生怎样变化？这个函数有最大值还是最小值？这个值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在△ABC中，已知DE∥BC，S△DOE：S△COB=4：9，求AD：AB的值．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷（解析版） 题型：解答题

    何老师安排喜欢探究问题的小明解决某个问题前，先让小明看了一个有解答过程的例题．

    例：若m2+2mn+2n2﹣6n+9=0，求m和n的值．

    【解析】
    ∵m2+2mn+2n2﹣6n+9=0

    ∴m2+2mn+n2+n2﹣6n+9=0

    ∴（m+n）2+（n﹣3）2=0

    ∴m+n=0，n﹣3=0∴m=﹣3，n=3

    为什么要对2n2进行了拆项呢？

    聪明的小明理解了例题解决问题的方法，很快解决了下面两个问题．相信你也能很好的解决下面的这两个问题，请写出你的解题过程．．

    解决问题：

    （1）若x2﹣4xy+5y2+2y+1=0，求xy的值；

    （2）已知a、b、c是△ABC的三边长，满足a2+b2=10a+12b﹣61，c是△ABC中最短边的边长，且c为整数，那么c可能是哪几个数？

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷（解析版） 题型：解答题

    计算：

    (1)|－1|+(—2)3+(7－π)0－()－1；

    (2) (－2a)3·(a2)2÷a3

    (3) (3a+b－2)(3a－b+2)

    (4)10002－1002×998

    (5) (x＋1)(x2＋1)(x4＋1)(x－1)

    (6) (3a+2)2(3a－2)2

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷（解析版） 题型：选择题

    下列各式中与2mn﹣m2﹣n2相等的是（ ）

    A．（m+n）2 B．﹣（m+n）2 C．（m﹣n）2 D．﹣（m﹣n）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．我们规定：平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d，点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D，定义点A到图形G的距离跨度为R=D-d．
    （1）①如图1，在平面直角坐标系xOy中，图形G1为以O为圆心，2为半径的圆，直接写出以下各点到图形G1的距离跨度：
    A（-1，0）的距离跨度；
    B（$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$）的距离跨度；
    C（-3，2）的距离跨度；
    ②根据①中的结果，猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是圆．
    （2）如图2，在平面直角坐标系xOy中，图形G2为以C（1，0）为圆心，2为半径的圆，直线y=k（x+1）上存在到G2的距离跨度为2的点，求k的取值范围．
    （3）如图3，在平面直角坐标系xOy中，射线OA：y=$\frac{\sqrt{3}}{3}$x（x≥0），圆C是以3为半径的圆，且圆心C在x轴上运动，若射线OA上存在点到圆C的距离跨度为2，直接写出圆心C的横坐标xc的取值范围．

    查看答案和解析>>

    同步练习册答案