
 如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)
如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)分析 (1)由t表示出PC及CQ的长,根据四边形PQBD为平行四边形可知∠PQC=∠ABC,故tan∠PQC=tan∠ABC,求出t的值即可;
(2)根据PD∥BC可得出△ADP∽△ABC,故$\frac{AP}{AC}$=$\frac{DP}{BC}$,由此可用t表示出DP的长,根据y=S梯形BCPD-S△PCQ即可得出结论;
(3)根据S四边形PQBD:S△ABC=3:8可直接得出t的值.
解答 解:(1)∵BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,
∴PC=6-t,CQ=2t,
∵四边形PQBD为平行四边形,
∴∠PQC=∠ABC,
∴tan∠PQC=tan∠ABC,即$\frac{PC}{QC}$=$\frac{AC}{BC}$,即$\frac{6-t}{2t}$=$\frac{6}{8}$,解得t=$\frac{12}{5}$(秒).
答:当t=$\frac{12}{5}$秒时,四边形PQBD为平行四边形;
(2)∵PD∥BC,
∴△ADP∽△ABC,
∴$\frac{AP}{AC}$=$\frac{DP}{BC}$,即$\frac{t}{6}$=$\frac{DP}{8}$,解得DP=$\frac{8t}{6}$,
∴y=S梯形BCPD-S△PCQ=$\frac{1}{2}$($\frac{8t}{6}$+8)•(6-t)-$\frac{1}{2}$×2t×(6-t)=$\frac{1}{3}$t2-6t+24(0<t<4);
(3)存在.
∵S四边形PQBD:S△ABC=3:8,S△ABC=$\frac{1}{2}$×8×6=24,
∴S四边形PQBD=$\frac{24×3}{8}$=9.
∵由(2)知,S四边形PQBD=$\frac{1}{3}$t2-6t+24,
∴$\frac{1}{3}$t2-6t+24=9,解得t=3或t=15,不合题意,
∴当t=3时,使S四边形PQBD:S△ABC=3:8.
点评 本题考查的是四边形综合题,涉及到相似三角形的判定与性质、梯形及三角形的面积公式等知识,难度适中.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
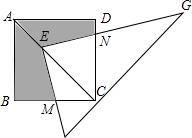 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,每个小正方形的边长为1,△ABC各顶点都在格点上,点A、C的坐标分别为(-1,2)、(0,-1),结合所给的平面直角坐标系解答下列问题:
如图,在平面直角坐标系中,每个小正方形的边长为1,△ABC各顶点都在格点上,点A、C的坐标分别为(-1,2)、(0,-1),结合所给的平面直角坐标系解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?
如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
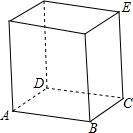 如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.
如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.| A. | $\frac{200}{3}$ | B. | $\frac{400}{3}$ | C. | $\frac{500}{3}$ | D. | $\frac{700}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.
如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
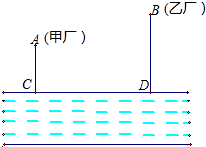 如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?
如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com