
分析 分两种情况:①当4$\sqrt{2}$是腰和10$\sqrt{2}$时,两边的和小于第三边,不能构成三角形,应舍去.②当4$\sqrt{2}$是底边和10$\sqrt{2}$是腰时,等腰三角形的周长就可以求出,进而可知正方形的周长、边长,就可以求出对角线长.
解答 解:①当4$\sqrt{2}$是腰长、10$\sqrt{2}$是底边长时,两边的和小于第三边,不能构成三角形,应舍去.
②当4$\sqrt{2}$是底边和10$\sqrt{2}$是腰时,
等腰三角形的周长是24$\sqrt{2}$,因而可得正方形的边长是6$\sqrt{2}$,
故这个正方形的对角线长是6$\sqrt{2}$÷cos45°=12;
故答案为:12.
点评 本题主要考查二次根式应用,是一个已知等腰三角形的边长求周长问题,需要进行讨论,同时应该考虑到三角形的三边关系定理,这是解决这类问题容易忽视的一点.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
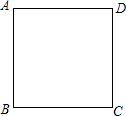 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
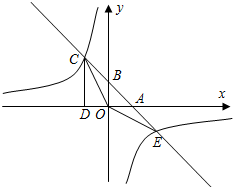 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.
已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
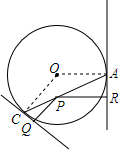 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
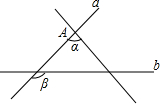 如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.
如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
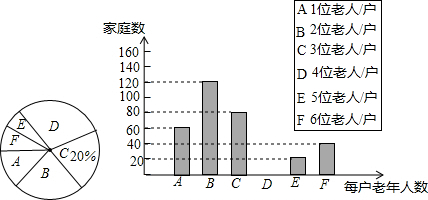
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.
如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com