
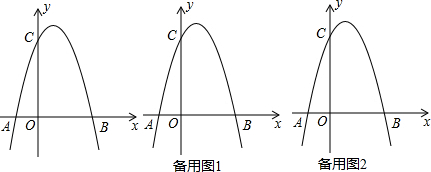
���� ��1�������A��B���꣬���ô���ϵ�������ɽ�����⣮
��2����ͼ1�У������ֱ��BD�Ľ���ʽΪ��y=-3x+12����Q��a��-3a+12������BH=4-a��QH=-3a+12������tan��NBH-tan��MQH=3�г��������a�����NH��HQ���ɽ�����⣮
��3����ͼ2�У���DF��AB��F��AM��BD��M��NQ��BD��AD��N��PE��AB��E������֤��NP=NQ����DQ=AP=a���ɴ��г��������a�����������P��Q���������⣮
��� �⣺��1���߶Գ���x=-$\frac{-2a}{2a}$=1����AB=6��
��A��-2��0����B��4��0����
�߰�B��4��0������������y=ax2-2ax+8�еã�16a-8a+8=0��
��a=-1��
��2����ͼ2�У������߽���ʽΪ��y=-x2+2x+8��
y=-��x2-2x+1-1��+8=-��x-1��2+9��
��D��1��9����
��ֱ��BD�Ľ���ʽΪ��y=kx+b��
��B��4��0����D��1��9������y=kx+b�еã�$\left\{\begin{array}{l}{4k+b=0}\\{k+b=9}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{k=-3}\\{b=12}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪ��y=-3x+12��
��Q��a��-3a+12������BH=4-a��QH=-3a+12��
��tan��NBH-tan��MQH=3��
��$\frac{NH}{4-a}$-$\frac{6}{-3a+12}$=3��
��NH=-3a+14��
��QN=NH-QH=��-3a+14��-��-3a+12��=2��
��3����ͼ2�У���DF��AB��F��AM��BD��M��NQ��BD��AD��N��PE��AB��E��
�ߡ�DPQ+��PQB=90�㣬��PQB=��DPQ+��PDQ��
��2��DPQ+��PDQ=90�㣮
�ߡ�PDQ+��DNQ=90�㣬
���DNQ=2��DPQ=��DPQ+��NQP��
���NPQ=��NQP��
��NP=NQ����DQ=AP=a��
��DA=DB��DF��AB��
��AF=FB=3����DF=9
��DA=DB=3$\sqrt{10}$��
��$\frac{1}{2}$•AB•DF=$\frac{1}{2}$•AM•DB��
��AM=$\frac{DF•AB}{DB}$=$\frac{9}{5}$$\sqrt{10}$��DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=$\frac{12}{5}$$\sqrt{10}$��
��NQ��AM��
��$\frac{NQ}{AM}$=$\frac{DQ}{DM}$=$\frac{DN}{AD}$��
��NQ=$\frac{3}{4}$a��DN=$\frac{5}{4}$a��
��PN=NQ��
��3$\sqrt{10}$-a-$\frac{5}{4}$a=$\frac{3}{4}$a��
��a=$\sqrt{10}$��
��PE��DF��
��$\frac{PE}{DF}$=$\frac{AP}{AC}$=$\frac{AO}{AF}$��
��AO=1��PO=3��
���P���꣨-1��3����
��QH��DF��
��$\frac{QH}{DF}$=$\frac{BQ}{DB}$=$\frac{BH}{BF}$
��$\frac{QH}{9}$=$\frac{2\sqrt{10}}{3\sqrt{10}}$=$\frac{BH}{3}$
��QH=6��BH=2��
���Q���꣨2��6������N���꣨2��8����
�������߽���ʽΪ��y=-x2+2x+8��
��x=2ʱ��y=8��
���N���������ϣ�
���� ���⿼����κ����ۺ��⡢һ�κ�����������Ǻ��������ɶ������������֪ʶ������Ĺؼ���ѧ�����ò������������̽�����⣬ѧ�����ӳ��ø����ߣ���Ҫ����Ӧ��ƽ���߷��߶γɱ��������������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1200}{x+40}$=$\frac{800}{x}$ | B�� | $\frac{1200}{x-40}$=$\frac{800}{x}$ | C�� | $\frac{1200}{x}$=$\frac{800}{x-40}$ | D�� | $\frac{1200}{x}$=$\frac{800}{x+40}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4x-3x=1 | B�� | x2+x2=2x4 | C�� | ��x2��3=x6 | D�� | 2x2•x3=2x6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
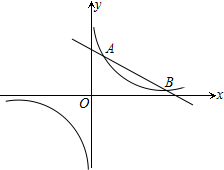 ��ͼ��˫����$y=\frac{k}{x}$��k��0����ֱ��$y=-\frac{1}{2}x+4$�ཻ��A��B����
��ͼ��˫����$y=\frac{k}{x}$��k��0����ֱ��$y=-\frac{1}{2}x+4$�ཻ��A��B�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ����в��ϣ�
�Ķ����в��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij������������Ϊ���˽Ȿ�ؾ��꼶ѧ��ÿ�ܡ��������������ʱ���������������˱��ز��־��꼶ѧ�������ռ��������ݽ����������Ƴ�����������ͳ֭ͼ��ѧ�����������������ʱ��x��h����Ϊ����ȼ���A��x��4����B��4��x��6����C��6��x��8����D��8��x��l0����E��x��10����
ij������������Ϊ���˽Ȿ�ؾ��꼶ѧ��ÿ�ܡ��������������ʱ���������������˱��ز��־��꼶ѧ�������ռ��������ݽ����������Ƴ�����������ͳ֭ͼ��ѧ�����������������ʱ��x��h����Ϊ����ȼ���A��x��4����B��4��x��6����C��6��x��8����D��8��x��l0����E��x��10�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com