
【题目】已知数轴上A. B两点对应的数分别为4和2,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A.点B的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到点A. 点B的距离之和为10?若存在,求出x的值;若不存在,请说明理由;
(3)若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问:多少分钟后P点到点A点B的距离相等?(直接写出结果)
![]()
【答案】(1)-1; (2)x=-6或4;(3)t=2
【解析】
(1)根据点P到点A、点B的距离相等,结合数轴可得答案;
(2)此题要分两种情况:①当P在AB左侧时,②当P在AB右侧时,然后再列出方程求解即可;
(3)根据题意可得无论运动多少秒,PB始终距离为2,且P在B的左侧,因此A也必须在A的左侧,才有P点到点A、点B的距离相等,设运动t分钟后P点到点A、点B的距离相等,表示出AP的长,然后列出方程即可.
(1)∵A、B两点对应的数分别为4和2,
∴AB=6,
∵点P到点A. 点B的距离相等,
∴P到点A. 点B的距离为3,
∴点P对应的数是1;
(2)存在;
设P表示的数为x,
①当P在AB左侧,PA+PB=10,
4x+2x=10,
解得x=6,
②当P在AB右侧时,
x2+x(4)=10,
解得:x=4;
(3)∵点B和点P的速度分别为1、1个长度单位/分,
∴无论运动多少秒,PB始终距离为2,
设运动t分钟后P点到点A. 点B的距离相等,
|4+2t|+t=2,
解得:t=2.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B’处;将三角形NAE沿EN折叠,点A落在点A’处.
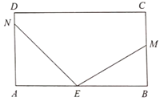
(1)若![]() ,
,![]() ,用直尺、量角器画出射线EB’与EA’;
,用直尺、量角器画出射线EB’与EA’;
(2)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
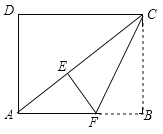
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
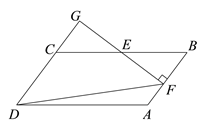
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.
(1)分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;
(2)校团委选择哪家印刷公司比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上![]() 两点相距
两点相距![]() 个单位长度,机器人从
个单位长度,机器人从![]() 点出发去
点出发去![]() 点,
点,![]() 点在
点在![]() 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进![]() 个单位长度,第二次它后退
个单位长度,第二次它后退![]() 个单位长度,第三次再前进
个单位长度,第三次再前进![]() 个单位长度,第四次又后退
个单位长度,第四次又后退![]() 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() ,那么
,那么
(1)求出![]() 点在数轴上表示的数.
点在数轴上表示的数.
(2)经过第七次行进后机器人到达点![]() ,第八次行进后到达点
,第八次行进后到达点![]() ,点
,点![]() 到
到![]() 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.
(3)机器人在未到达![]() 点之前,经过
点之前,经过![]() 次(
次(![]() 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含![]() 的代数式表示?
的代数式表示?
(4)如果![]() 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依次类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
则:(1)等比数列3,6,12,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a3,…是等比数列,且公比为q,那么根据定义可得到:
![]() ,……
,…… ![]() .
.
∴a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q= a1q3,……
由此可得:an= (用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com