
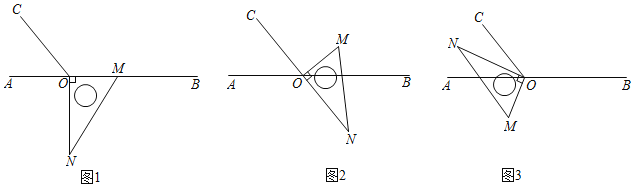
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC= °;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
【答案】(1)75°;(2)∠AOM﹣∠NOC=30°,理由详见解析;(3)三角板绕点O的运动时间为12秒或48秒.
【解析】
(1)由已知点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,可求出∠BOC的度数,由旋转的度数可以求出∠MOC的度数;
(2)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,然后作差即可;
(3)求得∠AOC=60°,则∠AOD=30°或∠AON=30°,即逆时针旋转60°或240°时直线ON平分∠AOC,据此求解.
解:(1)∵∠BOC+∠AOC=180°,∠BOC=2∠AOC,
∴∠AOC=60°,∠BOC=120°,
由旋转可知∠BOM=45°,
∴∠MOC=120°﹣45°=75°.
故答案为:75.
(2)由(1)得∠AOC=60°,
∵∠MON=90°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
∴∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.
(3)由(1)得∠AOC=60°,
①如下图,
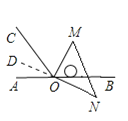
延长NO,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即逆时针旋转60°时NO延长线平分∠AOC,
由题意得,5t=60,
∴t=12;
②如下图,
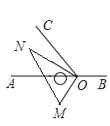
当NO平分∠AOC,
∴∠AON=30°,
即逆时针旋转240°时NO平分∠AOC,
∴5t=240,
∴t=48,
∴三角板绕点O的运动时间为12秒或48秒.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
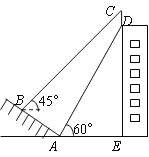
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①画射线BA;连接BD;
②画直线AD、BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF;
(2)点B与直线AD的关系是 ;
(3)图中以E为顶点的角中,小于平角的角共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
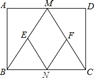
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB:AD= 时,四边形MENF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com