
【题目】如图,在![]() 中,
中,![]() ,且
,且![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() .①
.①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则下列结论正确的是________.
.则下列结论正确的是________.
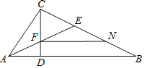
【答案】①②③④
【解析】
根据已知条件可证△ADC∽△CDB,得出∠ACB=90°.根据等量关系及等腰三角形的性质得到CF=BN.根据同位角相等,证明FN∥AB.证明△ADF∽△CDA,根据相似三角形的性质得出AD2=DFDC.
②∵CD⊥AB,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴△ADC∽△CDB,
∴∠ACD=∠B,
∴![]() ,故本选项正确;
,故本选项正确;
①∵AE平分∠CAB
∴∠CAE=∠DAF,
![]()
∴△CAE∽△DAF,
∴∠AFD=∠AEC,
∴∠CFE=∠AEC,
∴CF=CE,
∵CN=BE,
∴CE=BN,
∴CF=BN,故本选项正确;

③∵∠EAB=∠B,
∴EA=EB,
∵∠ACD=∠B,∠CAE=∠EAB,
∴∠ACD=∠CAE,
∴FA=FC,
∴FA=FC=BN,
EF=EN,
![]()
∠FEN=∠AEB,
∴△EFN∽△EAB,
∴∠EFN=∠EAB,
∴FN∥AB,故本选项正确;
④易证△ADF∽△CDA,
∴![]() 故本选项正确;
故本选项正确;
故答案为:①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若正整数n使得在计算n+(n+1)+(n+2)的过程中,个数位上均不产生进为现象,则称n为“本位数”,例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到奇数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.

(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.
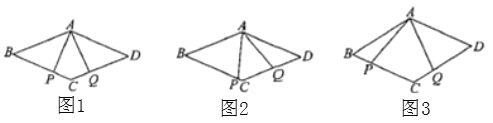
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.
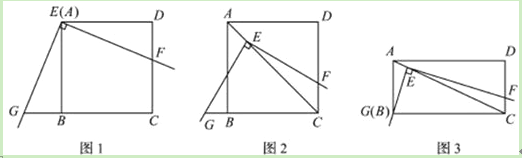
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .过点
.过点![]() 且与直线
且与直线![]() 平行的直线交
平行的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
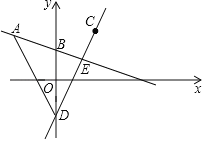
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,它与坐标轴分别交于A,B两点.
,它与坐标轴分别交于A,B两点.
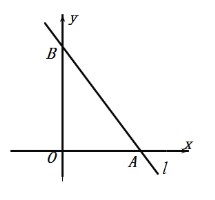
(1)求出点A的坐标;
(2)动点C从y轴上的点![]() 出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得
出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )
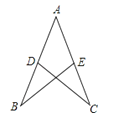
A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com