
分析 ①根据二次根式的加减法和除法可以解答本题;
②根据二次根式乘除法和减法可以解答本题;
③先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:①(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
=$(6\sqrt{3}-\frac{2\sqrt{3}}{3}+4\sqrt{3})÷2\sqrt{3}$
=3-$\frac{1}{3}$+2
=$4\frac{2}{3}$;
②$\frac{\sqrt{12}+\sqrt{27}}{\sqrt{3}}$-($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)
=$\sqrt{4}+\sqrt{9}-(3-2\sqrt{6}+2)$
=2+3-5+2$\sqrt{6}$
=2$\sqrt{6}$;
③($\frac{{a}^{2}-5a+2}{a+2}$+1)÷$\frac{{a}^{2}-4}{{a}^{2}+4a+4}$
=$\frac{{a}^{2}-5a+2+a+2}{a+2}•\frac{(a+2)^{2}}{(a+2)(a-2)}$
=$\frac{{a}^{2}-4a+4}{a-2}$
=$\frac{(a-2)^{2}}{a-2}$
=a-2,
当a=2+$\sqrt{3}$时,原式=2+$\sqrt{3}$-2=$\sqrt{3}$.
点评 本题考查二次根式的化简求值、分式的化简求值,解答本题的关键是明确它们各自的计算方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 方程$\sqrt{x}$=4的根是x=±16 | |
| B. | 方程$\sqrt{2x+3}$=x的根是x1=3,x2=-1 | |
| C. | 方程$\sqrt{2x-1}$=x+1变形所得的有理方程是2x-1=x2+1 | |
| D. | 方程$\sqrt{x+1}$+1=0没有实数解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 93分 | B. | 85分 | C. | 96分 | D. | 78分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
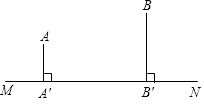 高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.
高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
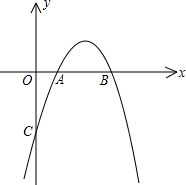 如图.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4.
如图.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
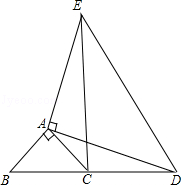 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
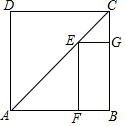 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com