
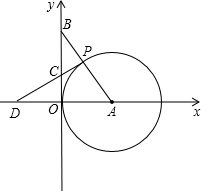
 点P,过点P作⊙A的切线交y轴于点C,交x轴于点D.
点P,过点P作⊙A的切线交y轴于点C,交x轴于点D.
|
| CO |
| DO |
| AP |
| DP |
| CO |
| 4 |
| 6 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3+q |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 9 |
| 4 |
| 3 |
| 8 |
| 147 |
| 8 |
| 147 |
| 8 |
| 21 |
| 8 |


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:
 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠a=75°,则b的值为
如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠a=75°,则b的值为5
| ||
| 3 |
5
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源:2013学年浙江省杭州市拱墅区第一学期期末教学质量调研九年级数学试卷(带解析) 题型:单选题
如图,已知A点坐标为(5,0),直线 与y轴交于点B,连接AB,若∠a=75°,则b的值为 ( )
与y轴交于点B,连接AB,若∠a=75°,则b的值为 ( ) 
| A.3 | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:2007年福建省福州一中高中招生(面向福州以外)综合素质测试数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com