
分析 把两个函数关系式联立成方程组求解,即可得到A(x1,y1)、B(x2,y2)两点的坐标,代入4x1y2-3x2y1求解即可.
解答 解:将y=ax代入y=$\frac{3}{x}$中整理得:ax2-3=0,
∵a≠0,
∴x2-$\frac{3}{a}$=0
∴x1,2=±$\frac{\sqrt{3a}}{a}$,y1,2=±$\sqrt{3a}$
$\left\{\begin{array}{l}{{x}_{1}=\frac{\sqrt{3a}}{a}}\\{{y}_{1}=\sqrt{3a}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{\sqrt{3a}}{a}}\\{{y}_{2}=-\sqrt{3a}}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{1}=-\frac{\sqrt{3a}}{a}}\\{{y}_{1}=-\sqrt{3a}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{\sqrt{3a}}{a}}\\{{y}_{2}=\sqrt{3a}}\end{array}\right.$
则4x1y2-3x2y1=4×$\frac{\sqrt{3a}}{a}$×(-$\sqrt{3a}$)-3×(-$\frac{\sqrt{3a}}{a}$)×$\sqrt{3a}$=-3
或4x1y2-3x2y1=4×(-$\frac{\sqrt{3a}}{a}$)×$\sqrt{3a}$-3×$\frac{\sqrt{3a}}{a}$×(-$\sqrt{3a}$)=-3
即:4x1y2-3x2y1=-3
故答案为:-3
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是把两个函数关系式联立成方程组求出两个交点的坐标.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
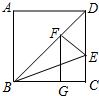 如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.
如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
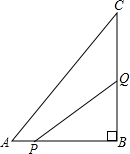 如图,在△ABC中,∠B=90°,AB=3厘米,BC=4厘米,点P从A沿AB边向点B以1厘米/秒的速度移动,点Q从B沿BC边向点C以2厘米/秒的速度移动,如P与Q同时出发,且当一点移动到端点并停止时,另一点也同时停下,1秒或2秒后三角形PBQ的面积为2平方厘米.
如图,在△ABC中,∠B=90°,AB=3厘米,BC=4厘米,点P从A沿AB边向点B以1厘米/秒的速度移动,点Q从B沿BC边向点C以2厘米/秒的速度移动,如P与Q同时出发,且当一点移动到端点并停止时,另一点也同时停下,1秒或2秒后三角形PBQ的面积为2平方厘米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com