
【题目】如图,已知△ABD、△BCE、△ACF都是等边三角形。

(1)试判断四边形ADEF的形状并说明理由.
(2)当△ABC满足_____,四边形ADEF是矩形(不需证明).
(3)当△ABC满足____,四边形ADEF是菱形(不需证明).
(4)当△ABC满足 ,四边形ADEF不存在. (不需证明).
【答案】(1)四边形ADEF是平行四边形,理由见解析; (2)∠BAC=150°;(3)AB=AC≠BC(AB=AC,∠BAC≠60°);(4)∠BAC=60°.
【解析】根据∠DBE=∠ABC,BD=BA,BE=BC,可证明△DBE≌△ABC,同理可证明△ABC≌△FEC,推出DE=AC=AF,FE=AB=AD,则四边形ADEF是个平行四边形.
解:(1)四边形ADEF是平行四边形.
易证△ABC≌△FEC,∴AB=FE.
∵△ABD是等边三角形,
∴AB=AD,∴AD=EF
同理可证△ABC≌△DBE,∴AC=DE.
∵△ACF是等边三角形,∴AC=AF,∴AF=DE
∴四边形ADEF是平行四边形.
(2)∠BAC=150°
(3)AB=AC≠BC(AB=AC,∠BAC≠60°)
(4)∠BAC=60°
“点睛”本题考查了等边三角形的性质,平行四边形的判定,全等三角形的性质和判定的应用,注意这些知识点的灵活运用.


科目:初中数学 来源: 题型:
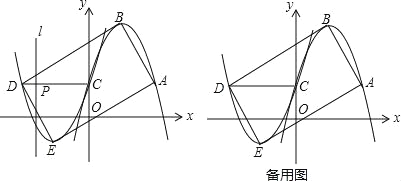
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯水价”文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
用水量(吨) | 15 | 20 | 25 | 30 | 35 |
户数 | 3 | 6 | 7 | 9 | 5 |
则这30户家庭该月用水量的众数和中位数分别是( )
A. 25,27 B. 30,25 C. 30,27 D. 25,25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com