
【题目】为了提倡“保护自然资源,节约自然资源”,某部门对某县一次性筷子的用量进行了调查.2015年从该县600家高、中、低档饭店中抽取了10家进行调查,得知这些饭店每天消耗的一次性筷子的盒数分别为:0.6,3.7,2.2,1.5,2.8,1.7,1.2,2.1,3.2,1.0.
(1)估计该县2015年各饭店共消耗多少盒一次性筷子?(一年按350个营业日计算)
(2)在(1)的条件下,若生产一套学生课桌椅需木材0.07 m3,则该县2015年各饭店使用一次性筷子所消耗的木材可以生产多少套学生课桌椅?(计算中需用到的有关数据为:每盒筷子100双,每双筷子的质量为5 g,所用木材的密度为0.5×103 kg/m3)
(3)通过以上计算,你对保护自然资源有什么看法?请提出两条合理的看法.
【答案】(1)420 000;(2)6 000;(3)①尽量减少使用一次性筷子;②加大对一次性筷子回收利用的力度.(答案不唯一)
【解析】
(1)首先求出样本的平均数,即为1家饭店1天消耗一次性木质筷子的盒数,然后再求出600家饭店350天消耗的一次性木质筷子的盒数.
(2)先求出一次性木质筷子的总质量420 000×100×5(kg),再求出木材的总体积约为:210 000÷(0.5×103),从而即可解题;
(3)联系实际提出合理的建议即可.
解:(1)样本的平均数![]() =
=![]() ×(0.6+3.7+2.2+1.5+2.8+1.7+1.2+2.1+3.2+1.0)=2(盒),因此该县2015年各饭店共消耗一次性筷子约2×350×600=420 000(盒).
×(0.6+3.7+2.2+1.5+2.8+1.7+1.2+2.1+3.2+1.0)=2(盒),因此该县2015年各饭店共消耗一次性筷子约2×350×600=420 000(盒).
(2)该县2015年各饭店使用一次性筷子所消耗的木材约为420 000×100×5=210 000 000(g)=210 000(kg),则木材的体积约为210 000÷(0.5×103)=420(m3),故可生产学生课桌椅约为420÷0.07=6 000(套).
(3)①尽量减少使用一次性筷子;②加大对一次性筷子回收利用的力度.(答案不唯一)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2+mx+n,直线y2=2x+1,抛物线y1的对称轴与直线y2的交点为点A,且点A的纵坐标为5.
(1)求m的值;
(2)若点A与抛物线y1的顶点B的距离为4,求抛物线y1的解析式;
(3)若抛物线y1与直线y2只有一个公共点,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
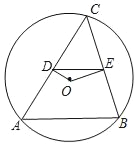
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3(a≠0)经过(1,0),且与y轴交于点C.
(1)直接写出点C的坐标 ;
(2)求a,b的数量关系;
(3)点D(t,3)是抛物线y=ax2+bx+3上一点(点D不与点C重合).
①当t=3时,求抛物线的表达式;
②当3<CD<4时,求a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣![]() <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com