
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD![]() DF,连接CF、BE.
DF,连接CF、BE.
(1)求证:DB![]() DE;
DE;
(2)求证:直线CF为⊙O的切线;
(3)若CF![]() 4,求图中阴影部分的面积.
4,求图中阴影部分的面积.

【答案】(1)(2)见解析;(3)![]()
【解析】分析:(1)欲证明DB=DE.,只要证明∠DBE=∠DEB;
(2)欲证明CF是⊙O的切线.,只要证明BC⊥CF即可;
![]() 根据S阴影部分
根据S阴影部分![]() S扇形
S扇形![]() S△OBD计算即可.
S△OBD计算即可.
详解:(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.
(2)连接CD.
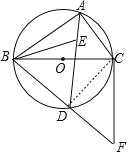
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴BD=CD,
又∵BD=DF,
∴CD=DB=DF,
∴![]()
∴BC⊥CF,
∴CF是⊙O的切线.
(3)连接OD.
∵O、D是BC、BF的中点,CF![]() 4, ∴OD
4, ∴OD![]() 2.
2.
∵CF是⊙O的切线,
∴![]()
∴△BOD为等腰直角三角形.
∴S阴影部分![]() S扇形
S扇形![]() S△OBD
S△OBD![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车分别在相距180千米的A、B两地相向而行,甲车每小时比乙车每小时快20千米,甲车在乙车出发2小时后出发,甲车出发1小时两车相遇。
(1)求甲、乙两车的速度各是多少?
(2)甲、乙两车各自到达目的地后都立即返回,问甲车从A地出发多长时间甲、乙两车 相距20千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负。一天中七次行驶记录如下。(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负。一天中七次行驶记录如下。(单位:![]() )
)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)求收工时距![]() 地多远?在
地多远?在![]() 地的什么方向?
地的什么方向?
(2)在第几次记录时离![]() 地最远,并求出最远距离。
地最远,并求出最远距离。
(3)若每千米耗油![]() 升。问共耗油多少升?
升。问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省嘉兴市,第20题,8分)如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点A(﹣1,2),B(m,﹣1).
)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,将正方形
上一点,将正方形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接并延长
处,连接并延长![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,求证:
,求证:![]()
(3)如图3,点![]() 分别在
分别在![]() 边上,点
边上,点![]() 分别在
分别在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言): ![]() .图2也是一种无限分割:在
.图2也是一种无限分割:在![]() 中,
中, ![]() ,
, ![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,又过点
,又过点![]() 作
作![]() 于点
于点![]() ,如此无限继续下去,则可将
,如此无限继续下去,则可将![]() 分割成
分割成![]() 、
、![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、….假设
、….假设![]() ,这些三角形的面积和可以得到一个等式是_________.
,这些三角形的面积和可以得到一个等式是_________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )
![]()
A. 13 cm B. 14 cm C. 15 cm D. 16 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com