
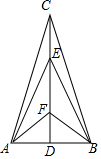
 如图,在△ABC中,AC=BC,CD是边AB上的高线,且有2CD=3AB=6,CE=EF=DF,则下列判断中不正确的是( )
如图,在△ABC中,AC=BC,CD是边AB上的高线,且有2CD=3AB=6,CE=EF=DF,则下列判断中不正确的是( )| A. | ∠AFB=90° | B. | BE=$\sqrt{5}$ | C. | △EFB∽△BFC | D. | ∠ACB+∠AEB=45° |
分析 由于AC=BC,CD是AB边上的高线,可知BD=1,且CD是AB的垂直平分线,利用2CD=3AB,易求CD=3,再利用垂直平分线的定理易求∠ACB=2∠BCE,∠AEB=2∠BEF,求出CE=EF=DF=1,易证△DBF是等腰直角三角形,再利用勾股定理可求BF=$\sqrt{2}$,可求$\frac{EF}{BF}$=$\frac{BF}{CF}$,而夹角相等易证△EFB∽△BFC,那么有∠FBE=∠BCF,∠FEB=∠FBC,结合三角形外角的性质易证∠ACB+∠AEB=90°.
解答 解:∵AC=BC,CD是AB边上的高线,3AB=6,
∴BD=AD=$\frac{1}{2}$AB=1,CD是AB的垂直平分线,
又∵2CD=3AB=6,AE=BE,AF=BF,
∴CD=3,∠ACB=2∠BCE,∠AEB=2∠BEF,
∵CE=EF=DF,
∴CE=EF=DF=1,
∴DF=DB=1,
又∵∠CDB=90°,
∴BE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,选项B正确,
△DBF、△DFA是等腰直角三角形,
∴∠DFB=∠DFA=45°,BF=$\sqrt{2}$,
∴∠AFB=90°,选项A正确,
$\frac{EF}{BF}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,$\frac{BF}{CF}$=$\frac{\sqrt{2}}{2}$,∴$\frac{EF}{BF}$=$\frac{BF}{CF}$,
又∵∠EFB=∠BFC,
∴△EFB∽△BFC,选项C正确,
∴∠FBE=∠BCF,∠FEB=∠FBC,
又∵∠DFB=∠FBE+∠FEB=∠FCB+∠FBC,
∴45°=∠FBE+∠FEB,
∴90°=2∠FBE+2∠FEB=2∠BCF+2∠FBC,
∴∠ACB+∠AEB=90°,选项D错误.
故选D.
点评 本题考查了等腰三角形的性质、勾股定理、等腰直角三角形的判定和性质、相似三角形的判定和性质、三角形外角的性质、线段垂直平分线的定理.关键是证明△EFB∽△BFC.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 方差 | C. | 平均数 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13,14 | B. | 14,14 | C. | 14,13.5 | D. | 14,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 买一张福利彩票一定中奖,是必然事件 | |
| B. | 买一张福利彩票一定中奖,是不可能事件 | |
| C. | 抛掷一个正方体骰子,点数为奇数的概率是$\frac{1}{3}$ | |
| D. | 有一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.01}<\root{3}{-5}$ | B. | $-\sqrt{10}<-\root{3}{30}$ | C. | $\frac{{\sqrt{10}}}{2}<\frac{{\sqrt{20}}}{3}$ | D. | $\sqrt{6}<2.4$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB=BC,∠ADC=60°,∠ABC=120°,连接BD,作AF⊥BD、AE⊥DC,垂足为F、E,BD、AE交于点O,下面的结论中,正确的有①②④.
如图,在四边形ABCD中,AB=BC,∠ADC=60°,∠ABC=120°,连接BD,作AF⊥BD、AE⊥DC,垂足为F、E,BD、AE交于点O,下面的结论中,正确的有①②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com