
【题目】如图,等腰三角形ABC中,AB=AC,P点在BC边上的高AD上,且![]() ,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.
,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.

【答案】2 4
【解析】
如果把△ABE与△ABC看作同高的两个三角形,那么它们的面积之比等于底之比,即等于AE:AC.所以为了求出△ABE的面积,由于已知S△ABC=10,只需求出AE:AC即可.为此,取EC中点F,连接DF.先由等腰三角形三线合一的性质得出D为BC中点,又F为EC中点,根据三角形中位线定理证出DF∥BE,再由平行线分线段成比例定理求出AE:EF,进而得出AE:AC,即可求S△ABE;根据S△BEC=S△ABC﹣S△ABE,先求出S△BEC,再根据三角形的中线将三角形的面积二等分,得出S△DEC.
解:如图所示,取EC中点F,连接DF.

∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵F为EC中点,
∴DF∥BE,则DF∥PE,
∴![]() ,
,
∴![]() =
=![]() .
.
∴![]() ,
,
∴S△ABE=![]() S△ABC=
S△ABC=![]() ×10=2;
×10=2;
∵S△BEC=S△ABC﹣S△ABE=10﹣2=8,
又∵D为BC中点,
∴S△DEC=![]() S△BEC=
S△BEC=![]() ×8=4.
×8=4.
故答案为2,4.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的4只小球,小球上分别标有1,2,3,4四个数字.
(1)从袋中随机摸出一只小球,求小球上所标数字为质数的概率;
(2)从袋中随机摸出一只小球,再从剩下的小球中随机摸出一只小球,求两次摸出的小球上所标数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m.鸡场的面积能达到150m2吗?如果能,请你给出设计方案;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
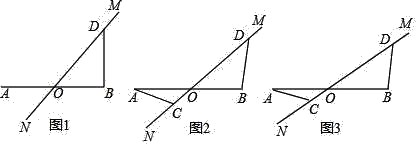
【题目】直线MN与线段AB相交于点O,点C、点D分别为射线ON,OM上两点,且满足∠ACN=∠ODB=45°.
(1)如图1,当点C与点O重合时,且AO=OB,请直接写出AC与BD的数量关系;
(2)将图1中的MN绕点O顺时针旋转α°(0<a<45),如图2所示,若AO=OB,(1)中的AC与BD的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若AO=kOB.
①请求出![]() 的值;
的值;
②若k=![]() ,∠AOC=30°,BD=3
,∠AOC=30°,BD=3![]() ,请直接写出OC的长.
,请直接写出OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与弧AB交于点D,以O为圆心,OC的长为半径作弧CE交OB于点E,若OA=6,∠AOB=120°,则图中阴影部分的面积为_________(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB与点E、DF⊥AC与点F.求证:DE= DF;
(2)如图2,等腰三角形ABC中,AB=AC=13,BC=10,点D是BC边上的动点,DE⊥AB与点E、DF⊥AC与点F.请问DE+DF的值是否随点D位置的变化而变化?若不变,请直接写出DE+DF的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为a+b的正方形图形分割成四部分(两个正方形和两个长方形),请认真观察图形,解答下列问题:
(1)根据图中条件,请用两种方法表示该图形的总面积(用含a、b的代数式表示出来);
(2)如果图中的a,b(a>b)满足a2+b2=57,ab=12,求a+b的值;
(3)已知(5+2x)2+(2x +3)2=60,求(5+2x)(2x+3)的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com