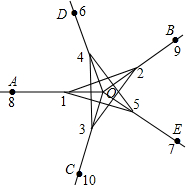
如图.平面内有公共端点的五条射线OA.OB.OC.OD.OE.从射线OA开始.在射线上写出数字1.2.3.4.5, 6.7.8.9.10.-．按此规律.则“14 在射线OE上,“2015 在射线OA上．题目和参考答案——青夏教育精英家教网—

6．

如图，平面内有公共端点的五条射线OA，OB，OC，OD，OE，从射线OA开始，在射线上写出数字1，2，3，4，5； 6，7，8，9，10，…．按此规律，则“14”在射线OE上；“2015”在射线OA上．

分析本题是一道关于数字变化猜想的问题，关键是通过归纳与总结，得到其中的规律．

解答解：∵如图所示可知，每隔一个数正好是连续的有理数，

∴11在OB上，12在射线OC上，13在射线OD上，
∴“14”在射线OE上．
∵每5个数一轮，
2015÷5=403，
每5轮顶点正好循环一周，403÷5=80余数为3，
∴“2015”与第3轮最后一个数的位置相同，
即与1的位置相同，
∴“2015”在射线 OA上．
故答案为：OE，OA．

点评此题主要考查了数字变化规律，解决问题的关键是通过归纳与总结，得到其中的规律．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

3．苹果的进价是每千克1.5元，销售中估计有5%的正常损耗，商家要获利10%，在每千克苹果售价至少为1.74（结果精确到0.01）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．先化简，再求值：$\frac{a+1}{a}$•$\frac{{a}^{2}}{{a}^{2}-1}$，其中a=5．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

1．

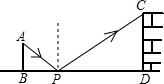如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是8米．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．观察下列等式：
第1个等式：a₁=$\frac{1}{1×3}$=$\frac{1}{2}$×（1-$\frac{1}{3}$）；
第2个等式：a₂=$\frac{1}{3×5}$=$\frac{1}{2}$×（$\frac{1}{3}$-$\frac{1}{5}$）；
第3个等式：a₃=$\frac{1}{5×7}$=$\frac{1}{2}$×（$\frac{1}{5}$-$\frac{1}{7}$）；
第4个等式：a₄=$\frac{1}{7×9}$=$\frac{1}{2}$×（$\frac{1}{7}$-$\frac{1}{9}$）；
…
请解答下列问题：
（1）按以上规律列出第n个等式：a_n=$\frac{1}{（2n-1）（2n+1）}$=$\frac{1}{2}$×（$\frac{1}{2n-1}-\frac{1}{2n+1}$）（n为正整数）．
（2）计算a_n+a_n+1的值（n为正整数）．
（3）直接写出a₁+a₂+a₃+a₄+…+a_n+1的值．
（4）参考题目中的规律，直接写出$\frac{1}{1×5}+\frac{1}{5×9}+\frac{1}{9×13}+…+\frac{1}{（4n-3）（4n+1）}$的运算结果．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

如图，将两张长为8宽为2的矩形纸条交叉，使重叠部分呈一个菱形，求菱形周长的最大值17．