
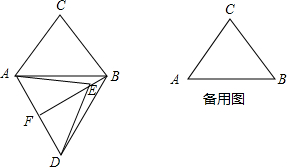
���� ��1��������ת����֪AB=AD����BAD=60�㼴�ɵ�֤������BA=BD��EA=ED�����д������ʼ��ɵ�֤���۷ֱ����BF��EF�ij����ɵã�
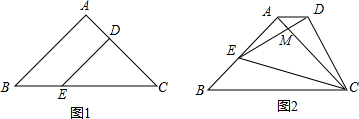
��2���ɡ�ACB+��BAC+��ABC=180�㡢��DAG+��DAE+��BAE=180�㡢��DAG=��ACB����DAE=��BAC�á�BAE=��BAC��AE=AC���������ߺ�һ�ɵ�CE��AB��AC=5��AH=3���̶�֪CE=2CH=8��BE=5�����ɵô𰸣�
��� �⣺��1���١ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60��õ���ADE��
��AB=AD����BAD=60�㣬
���ABD�ǵȱ������Σ�
���ɢٵá�ABD�ǵȱ������Σ�
��AB=BD��
�ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60��õ���ADE��
��AC=AE��BC=DE��
�֡�AC=BC��
��EA=ED��
���B��E��AD���д����ϣ�
��BE��AD���д��ߣ�
�ߵ�F��BE���ӳ����ϣ�
��BF��AD��AF=DF��
���ɢ�֪BF��AD��AF=DF��
��AF=DF=3��
��AE=AC=5��
��EF=4��
���ڵȱ�������ABD�У�BF=AB•sin��BAF=6��$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$��
��BE=BF-EF=3$\sqrt{3}$-4��
��2����ͼ��ʾ��
�ߡ�DAG=��ACB����DAE=��BAC��
���ACB+��BAC+��ABC=��DAG+��DAE+��ABC=180�㣬
�֡ߡ�DAG+��DAE+��BAE=180�㣬
���BAE=��ABC��
��AC=BC=AE��
���BAC=��ABC��
���BAE=��BAC��
��AB��CE����CH=HE=$\frac{1}{2}$CE��
��AC=BC��
��AH=BH=$\frac{1}{2}$AB=3��
��CE=2CH=8��BE=5��
��BE+CE=13��
���� ������Ҫ������ת�����ʡ��ȱ������ε��ж������ʡ��д��ߵ����ʡ��������ڽǺͶ�����֪ʶ�㣬����������ת�������ǽ���Ĺؼ���


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
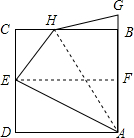 ��������ֽƬABCD����ͼ��ʾ���ۣ�ʹ��AD��BC�غϣ��ۺ�ΪEF������AE����AE�۵���AB�ϣ��ۺ�ΪAH����$\frac{BH}{BC}$��ֵ��$\frac{\sqrt{5}-1}{2}$��
��������ֽƬABCD����ͼ��ʾ���ۣ�ʹ��AD��BC�غϣ��ۺ�ΪEF������AE����AE�۵���AB�ϣ��ۺ�ΪAH����$\frac{BH}{BC}$��ֵ��$\frac{\sqrt{5}-1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
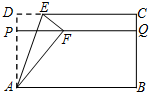 ��ͼ���ھ���ֽƬABCD�У�AD=12cm���ֽ�����ֽƬ������ͼʾ��ʽ�۵���AE���ۺۣ���DP=$\frac{1}{n}$AD��CQ=$\frac{1}{n}$BC����D�Ķ�Ӧ��F��PQ�ϣ���AE�ij���12$\sqrt{\frac{2n}{2n-1}}$cm��
��ͼ���ھ���ֽƬABCD�У�AD=12cm���ֽ�����ֽƬ������ͼʾ��ʽ�۵���AE���ۺۣ���DP=$\frac{1}{n}$AD��CQ=$\frac{1}{n}$BC����D�Ķ�Ӧ��F��PQ�ϣ���AE�ij���12$\sqrt{\frac{2n}{2n-1}}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
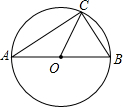 ��ͼ��AB�ǡ�O��ֱ����BC�ǡ�O���ң�����OBC=60�㣬���BAC�Ķ����ǣ�������
��ͼ��AB�ǡ�O��ֱ����BC�ǡ�O���ң�����OBC=60�㣬���BAC�Ķ����ǣ�������| A�� | 75�� | B�� | 60�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com