
【题目】如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F. 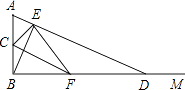
(1)求证:BF=FD;
(2)点D在运动过程中能否使得四边形ACFE为平行四边形?如不能,请说明理由;如能,求出此时∠A的度数.
【答案】
(1)证明:∵BE⊥AD,
∴∠AEB=90°,
在Rt△AEB中,∵点C为线段BA的中点,
∴CE= ![]() AB=CB,
AB=CB,
∴∠CEB=∠CBE.
∵∠CEF=∠CBF=90°,
∴∠BEF=∠EBF,
∴EF=BF.
∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,
∴∠FED=∠EDF,
∵EF=FD.
∴BF=FD
(2)能.理由如下:
若四边形ACFE为平行四边形,则AC∥EF,AC=EF,
∴BC=BF,
∴BA=BD,∠A=45°.
∴当∠A=45°时四边形ACFE为平行四边形.
【解析】(1)由直角三角形斜边上的中线性质得出CE=CB,由等腰三角形的性质和直角三角形的性质证出EF=BF,EF=FD,即可得出结论.(2)假设点D在运动过程中能使四边形ACFE为平行四边形,则AC∥EF,AC=EF,由(1)知AC=CB= ![]() AB,EF=BF=
AB,EF=BF= ![]() BD,则BC=EF=BF,即BA=BD,∠A=45°.
BD,则BC=EF=BF,即BA=BD,∠A=45°.
【考点精析】掌握平行四边形的判定是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
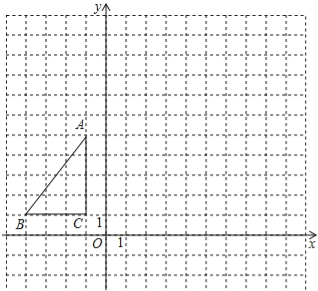
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 绝对值是它本身的数只有0 B. 如果几个数积为0,那么至少有一个因数为0
C. 整数只包括正整数和负整数 D. -1是最大的负有理数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日前,中国儿童文学作家曹文轩荣获2016年国际儿童读物联盟(IBBY)国际安徒生奖,新安书店抓住契机,以每本20元的价格购进一批畅销书《曹文轩作品集》.销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如下表所示,按照表中y与x的关系规律,解决下面的问题:

(1)试求出y与x的函数关系式。
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com