
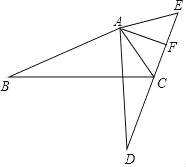
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
【答案】(1)证明见解析;(2)40°
【解析】
(1)由∠BAD=∠CAE可证得∠BAC=∠DAE,结合已知条件利用SAS证明△ABC≌△ADE; (2)根据三角形的内角和定理求得∠ACB=50°,利用全等三角形的性质可得∠ACB=∠AED=50°,由等腰三角形三线合一的性质可得AF⊥CE,即可求得∠FAE的度数.
(1)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS);
(2)∵∠B+∠ACB+∠BAC=180°,
∴∠ACB=180°-∠B-∠BAC=50°,
∵△ABC≌△ADE,
∴∠ACB=∠AED=50°,
∵点F是CE的中点,
∴AF⊥CE,
∴∠FAE=90°-∠E=40° .


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
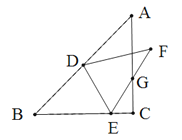
【题目】如图,△ABC中,∠ACB=90°,AB=2,BC=AC,D为AB的中点,E为BC上一点,将△BDE沿DE翻折,得到△FDE,EF交AC于点G,则△ECG的周长是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学第八届校园文化艺术节中,其中有三个年级老师参加的“校园歌手大奖赛”,艺术节组委会要求三个年级先进行预赛,选出男、女各一名选手参加决赛,七、八、九年级选手编号分别为男1号,女1号;男2号,女2号;男3号,女3号,比赛规则是男女各一人组成搭档进行决赛比赛.
(1)求是同一年级男、女教师选手组成搭档的概率.
(2)求低年级男教师与高年级女教师组成搭档的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标.
(2)若折叠后点B落在边OA上的点为B′,是否存在点B′,使得四边形BCB′D是菱形?若存在,请说明理由并求出菱形的边长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
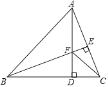
【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( ) 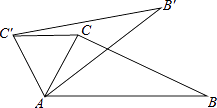
A.70°
B.35°
C.40°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司招标了一批灯箱加工工程,需要在规定时间内加工1400个灯箱,该公司按一定速度加工5天后,发现按此速度加工下去会延期10天完工,于是又抽调了一批工人投入灯箱加工,使工作效率提高了50%,结果如期完成工作.
(1)求该公司前5天每天加多少个灯箱;
(2)求规定时间是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D. 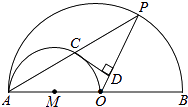
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com