
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
(1)若△BCD的周长为8,求BC的长;
(2)若∠A=40°,求∠DBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是 . 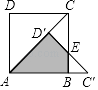
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x的图象为直线l.
(1)观察与探究
已知点A与A′,点B与B′分别关于直线l对称,其位置和坐标如图所示.请在图中标出C(4,﹣1)关于线l的对称点C′的位置,并写出C′的坐标_____;
(2)归纳与发现
观察以上三组对称点的坐标,你会发现:
平面直角坐标系中点P(a,b)关于直线l的对称点P′的坐标为_____;
(3)运用与拓展
已知两点M(﹣3,3)、N(﹣4,﹣1),试在直线l上作出点Q,使点Q到M、N两点的距离之和最小,并求出相应的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 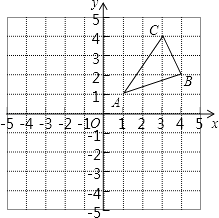
(1)①请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
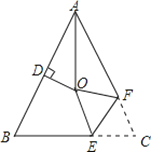
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 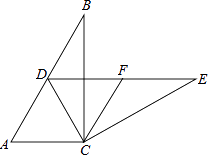
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com