解:(1)四边形EFPG是平行四边形.
理由:∵点E、F分别是BC、PC的中点,
∴EF∥BP.
同理可证EG∥PC.
∴四边形EFPG是平行四边形.
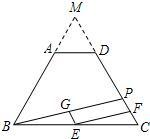
(2)方法一:当PC=3时,四边形EFPG是矩形.
证明:延长BA、CD交于点M.
∵AD∥BC,AB=CD,∠BAD=120°,
∴∠ABC=∠C=60°.
∴∠M=60°,
∴△BCM是等边三角形.
∵∠MAD=180°-120°=60°,
∴AD=DM=2.
∴CM=DM+CD=2+4=6.
∵PC=3,
∴MP=3,
∴MP=PC,
∴BP⊥CM即∠BPC=90度.
由(1)可知,四边形EFPG是平行四边形,
∴四边形EFPG是矩形.
方法二:当PC=3时,四边形EFPG是矩形.
证明:延长BA、CD交于点M.由(1)可知,四边形EFPG是平行四边形.
当四边形EFPG是矩形时,∠BPC=90度.
∵AD∥BC,∠BAD=120°,
∴∠ABC=60度.
∵AB=CD,∴∠C=∠ABC=60度.
∴∠PBC=30°且△BCM是等边三角形.
∴∠ABP=∠PBC=30°,
∴PC=PM=

CM.
同方法一,可得CM=DM+CD=2+4=6,
∴PC=6×

=3.
即当PC=3时,四边形EFPG是矩形.
分析:根据中点的条件,可以利用.三角形的中位线定理证明四边形EFPG的两组对边分别平行,得出这个四边形是平行四边形;
在平行四边形的基础上要说明四边形是矩形,只要再说明一个角是直角就可以.
点评:本题主要考查学生对等腰梯形的性质,平行四边形的判定及矩形的判定的理解及运用.

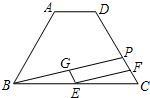 ,点E、F、G分别是线段BC、PC、BP的中点.
,点E、F、G分别是线段BC、PC、BP的中点.
 CM.
CM. =3.
=3.

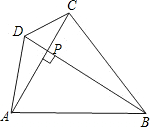
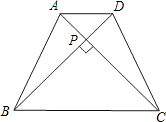
 (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4