
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
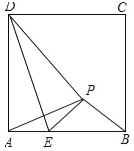
【答案】1或![]()
【解析】
分两种情况讨论:若AP=BP时,△ADP是等边三角形;若AP=AB时,点P在AB的垂直平分线上,且PF⊥AD,得到PF=![]() AB,在理折叠的性质和正方形性质即可解答
AB,在理折叠的性质和正方形性质即可解答
若AP=BP,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90°,
∵折叠
∴AD=DP=AP,∠ADE=∠PDE
∴△ADP是等边三角形
∴∠ADP=60°
∴∠ADE=30°
∴AE=![]() =
=![]()
若AP=AB,
如图,过点P作PF⊥AD于点F,作∠MED=∠MDE,
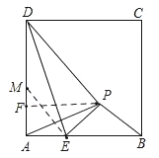
∵AP=PB,
∴点P在AB的垂直平分线上,且PF⊥AD,
∴PF=![]() AB,
AB,
∵折叠
∴AD=DP=AB,∠ADE=∠PDE
∴PF=![]() PD
PD
∴∠PDF=30°
∴∠ADE=15°
∵∠MED=∠MDE,
∴∠AME=30°,ME=MD
∴AM=![]() AE,ME=2AE
AE,ME=2AE
∴AD=2AE+![]() AE=2+
AE=2+![]()
∴AE=1
故答案为1或 ![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
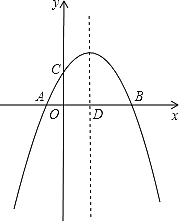
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的序号为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )

A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】B,C是⊙O上的两个定点,A是圆上的动点,0°<∠BAC<90°,BD∥AC,CD∥AB.
(1)如图1,如果△ABC是等边三角形,求证BD是⊙O的切线:
(2)如图2,如果60°<∠BAC<90°,BD,CD分别交⊙O于E,F,研究五边形ABEFC的性质;
①探索AE、AF和BC的数量关系,并证明你的结论:
②如图3,若⊙O的半径为4,∠BAC=75°,求边EF的长;
③若AB=c,AC=b,直接写出BE,CF的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)

(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.
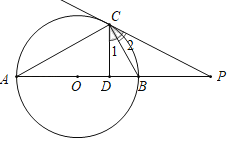
(1)求证:直线PC是⊙O的切线;
(2)若CD=4,BD=2,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB、AC为一边,向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”
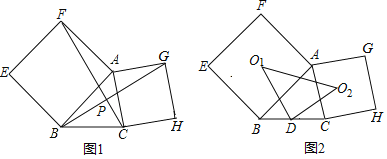
(1)如图1,连接BG,CF相交于点P,求证:BG=CF且BG⊥CF;
(2)如图2,点D是BC的中点,两个依伴正方形的中心分别为O1,O2连结O1D,O2D,O1O2:,判断△DO1O2的形状并说明由;
(3)如图2,若AB=6,AC=![]() ,∠BAC=60°,求O1O2的长.
,∠BAC=60°,求O1O2的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com