
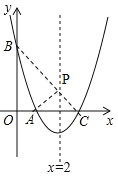
【题目】如图,抛物线![]() 交x轴于点
交x轴于点![]() ,交y轴于点B,对称轴是直线
,交y轴于点B,对称轴是直线![]() .
.
(1)求抛物线的解析式;
(2)P是抛物线对称轴上的一个动点,是否存在点P,使![]() 的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
()根据对称轴和点A坐标列方程组求出b、c的值即可得答案;(2)设C点为抛物线与x轴的另一个交点,连接![]() ,与
,与![]() 交于点P,根据二次函数的对称性可得PA=PC,点C坐标,根据两点之间,线段最短可得P点即为所求,利用待定系数法求出直线BC的解析式,把x=2代入即可求出P点坐标.
交于点P,根据二次函数的对称性可得PA=PC,点C坐标,根据两点之间,线段最短可得P点即为所求,利用待定系数法求出直线BC的解析式,把x=2代入即可求出P点坐标.
(1)由题意得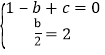 ,
,
解得![]() .
.
∴抛物线解析式为![]() .
.
(2)设C点为抛物线与x轴的另一个交点,连接![]() ,与
,与![]() 交于点P,
交于点P,
∵点A与点C关于x=2对称,A(1,0)
∴PA=PC,C(3,0)
∵两点之间,线段最短,
∴PA+PB+AB=BC+AB,即△PAB的周长为最小值.
∵x=0时,y=3,
∴B(0,3),
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
当x=2时,y=-2+3=1
∴![]() .
.
即存在点P,使![]() 的周长最小,点P坐标为(2,1).
的周长最小,点P坐标为(2,1).


科目:初中数学 来源: 题型:
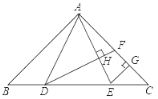
【题目】如图,在△ABC中,AB=AC,点D、E在线段BC上,且BE=CD,连接AD、AE,过点D作DF⊥AE,垂足为H,交AC于点F,过点E作EG⊥AC,垂足为G.
(1)若DH=4,AD=5,HF=1,求AF的长;
(2)若∠BAC=90°,求证:AF=2CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用900元正好可以购进50个甲种零件和50个乙种零件.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出该五金商店本次从机械厂购进甲、乙两种零件有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学公益组织计划购买![]() 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元.
套装共需820元.
(1)求购买一套![]() 套装文具、一套
套装文具、一套![]() 套装各需要多少元?
套装各需要多少元?
(2)根据该公益组织的募捐情况和捐助对象情况,需购买![]() 两种套装共60套,要求购买
两种套装共60套,要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多多少套?
套装最多多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春华中学为了解九年级学生的身高情况,随机抽测50名学生的身高后,所得部分资料如下(身高单位:![]() ,测量时精确到
,测量时精确到![]() ):
):
身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
若将数据分成8组,取组距为![]() ,相应的频率分布表(部分)是:
,相应的频率分布表(部分)是:
分组 | 频数 | 频率 |
147.5~151.5 | 2 | 0.04 |
151.5~155.5 | 3 | 0.06 |
155.5~159.5 | 5 | 0.10 |
159.5~163.5 | 11 | 0.22 |
163.5~167.5 | ________ | ________ |
167.5~171.5 | 7 | 0.14 |
171.5~175.5 | 4 | 0.08 |
175.5~179.5 | 2 | 0.04 |
合计 | 50 | 1.00 |
请回答下列问题:
(1)样本数据中,学生身高的众数、中位数各是多少?
(2)填写频率分布表中未完成的部分;
(3)若该校九年级共有850名学生,请你估计该年级学生身高在![]() 及以上的人数.
及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
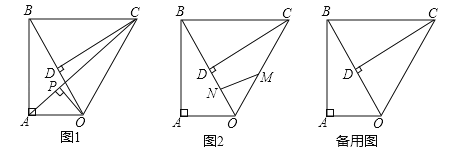
【题目】已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,如图1,连接
,如图1,连接![]() .
.
(1)填空:![]()
![]() ;
;
(2)如图1,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,点![]() ,
,![]() 同时从点
同时从点![]() 出发,在
出发,在![]() 边上运动,
边上运动,![]() 沿
沿![]() 路径匀速运动,
路径匀速运动,![]() 沿
沿![]() 路径匀速运动,当两点相遇时运动停止,已知点
路径匀速运动,当两点相遇时运动停止,已知点![]() 的运动速度为1.5单位
的运动速度为1.5单位![]() 秒,点
秒,点![]() 的运动速度为1单位
的运动速度为1单位![]() 秒,设运动时间为
秒,设运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求当
,求当![]() 为何值时
为何值时![]() 取得最大值?最大值为多少?
取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com