
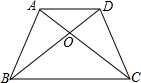
 等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值.
等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值. 解:过点D作DE∥AC,交BC的延长线于点E,作DF⊥BE于点F,
解:过点D作DE∥AC,交BC的延长线于点E,作DF⊥BE于点F,
| ||
| 2 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;
用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )A、1
| ||
B、
| ||
| C、2 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知a、b、c为有理数,且它们在数轴上的位置如图所示.
已知a、b、c为有理数,且它们在数轴上的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( )| A、2 | B、3 | C、4 | D、5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com