
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
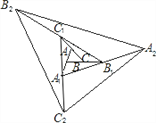
A. 6 B. 5 C. 4 D. 3
【答案】C
【解析】试题分析:先根据已知条件求出△A1B1C1及△A2B2C2的面积,再根据两三角形的倍数关系求解即可.
解:△ABC与△A1BB1底相等(AB=A1B),高为1:2(BB1=2BC),故面积比为1:2,
∵△ABC面积为1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证△A2B2C2的面积=7×△A1B1C1的面积=49,
第三次操作后的面积为7×49=343,
第四次操作后的面积为7×343=2401.
故按此规律,要使得到的三角形的面积超过2015,最少经过4次操作.
故选C.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
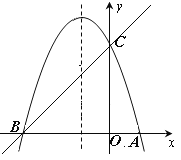
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂一月份生产某机器100台,计划二、三月份共生产280台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )
A.100(1+x)2=280
B.100(1+x)+100(1+x)2=280
C.100(1﹣x)2=280
D.100+100(1+x)+100(1+x)2=280
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:
(1)乘积是1的两个数互为______;
(2)有理数的除法法则,除以一个数等于乘以这个数的______;
(3)两数相除,同号得______,异号得______,并把绝对值______,0除以任何一个不等于0的数都得______.
查看答案和解析>>
科目:初中数学 来源: 题型:
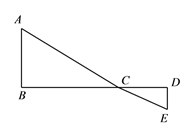
【题目】如图, ![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 、
、![]() 作
作![]() ,
, ![]() ,连接
,连接![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)请问点![]() 在什么位置时,
在什么位置时, ![]() 的值最小,求出这个最小值;
的值最小,求出这个最小值;
(3)根据(2)中的规律和结论,构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com