
| 作物名称 | 蔬菜 | 果树 | 药材 |
| 每亩地所需的人数(人) | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 每亩地的预测利润(元) | 11000 | 7500 | 6000 |
分析 设种植蔬菜的人数为x人,种植果树的为y人,种植药材的为z人,根据总人数为40以及承包土地为100亩,即可得出关于x、y、z的三元一次方程组,用含z的代数式分别表示出x、y,设利润总和为w元,根据总利润=种植蔬菜利润+种植果树利润+种植药材利润,即可得出w关于x的函数关系式,由x、y、z的范围可确定z的取值范围,再利用一次函数的性质即可确定w取最大值是z的值,将其分别代入x、y中,此题得解.
解答 解:设种植蔬菜的人数为x人,种植果树的为y人,种植药材的为z人,
根据题意得:$\left\{\begin{array}{l}{x+y+z=40}\\{2x+3y+4z=100}\end{array}\right.$,
∴y=20-2z,x=20+z.
设利润总和为w元,
根据题意得:w=11000×2x+7500×3y+6000×4z=1000z+890000.
∵0<x<40,0<y<40,0<z<40,
即$\left\{\begin{array}{l}{0<20-2z<40}\\{0<20+z<40}\\{0<z<40}\end{array}\right.$,解得:0<z<10.
∵w随z的值增大而增大,
∴当z=9时,w取最大值,最大值为1000×9+890000=899000,
此时y=20-2z=2,x=20+z=29.
答:种植方案为:种植蔬菜29人、种植果树2人、种植药材9人.
点评 本题考查了一次函数的应用、三元一次方程组以及解一元一次不等式组,根据数量关系找出w关于z的函数关系式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 9.5359×1011 | B. | 95.359×1010 | C. | 0.95359×1012 | D. | 9.5×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
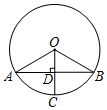 如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | $\frac{9}{2}$ cm | B. | $\frac{3\sqrt{3}}{2}$cm | C. | 3$\sqrt{3}$cm | D. | $\frac{9}{4}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2013}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2015}{4032}$ | D. | $\frac{2017}{4032}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com