
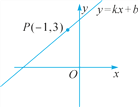
【题目】如图,直线y=kx+b上有一点P(-1,3),回答下列问题:
(1)关于x的方程kx+b=3的解是_______.
(2)关于x的不等式kx+b>3的解是________.
(3)关于x的不等式kx+b-3<0的解是______.
(4)求不等式-3x≥kx+b的解.
(5)求不等式(k+3)x+b>0的解.
【答案】(1)x=-1;(2)x>-1;(3)x<-1;(4)x≤-1;(5)x>-1.
【解析】试题分析:(1)利用一次函数图像性质与一元一次方程的关系.(2)(3)(4)
(5)利用一次函数图像性质与一元一次不等式的关系
试题解析:(1)因为P(-1,3)在一次函数y=kx+b图像上,所以kx+b=3得解为x=-1.
(2) 不等式kx+b>3,恰好是一次函数y=kx+b函数值大于3的部分,对应的x>-1.
(3)因为 kx+b-3<0所以kx+b<3, 恰好是一次函数y=kx+b函数值大小于3的部分对应的x<-1.
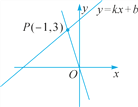
(4)观察图象可知,点(-1,3)在函数y=-3x上,构造函数y=-3x如解图.y=-3x比y=kx+b图像“高”的部分,
∴不等式-3x≥kx+b的解为x≤-1.
(5)不等式(k+3)x+b>0可变形为kx+b>-3x,仿照(4)可得x>-1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.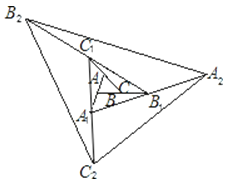
A.6
B.5
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医院为支援武汉,经自愿申请遴选了5名医护人员组成“志愿小分队”,5名医护人员的年龄分别为(单位:岁)24,25,24,27,32.则这组数据的中位数和众数分别是( )
A.24岁和24岁B.25岁和24岁C.25岁和27岁D.26岁和27岁
查看答案和解析>>
科目:初中数学 来源: 题型:
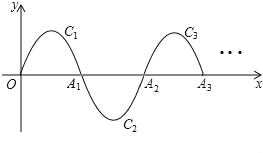
【题目】一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com