
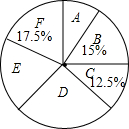
 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 40 | 60 | 100 |
| A. | 这次被调查的学生人数为400人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中喜欢选修课E、F的人数分别为80,70 | |
| D. | 喜欢选修课C的人数最少 |
分析 通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
解答 解:被调查的学生人数为60÷15%=400(人),
∴选项A正确;
扇形统计图中D的圆心角为$\frac{100}{400}$×360°=90°,
∵$\frac{40}{400}$×360°=36°,360°×(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°-162°-90°-36°=72°,
∴选项B正确;
∵400×$\frac{72°}{360°}$=80(人),400×17.5%=70(人),
∴选项C正确;
∵12.5%>10%,
∴喜欢选修课A的人数最少,
∴选项D错误;
故选:D.
点评 本题考查了条形统计图、扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
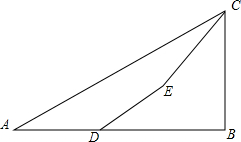 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
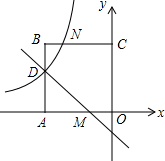 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=$\frac{m}{x}$的图象经过点D,与BC的交点为N.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=$\frac{m}{x}$的图象经过点D,与BC的交点为N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
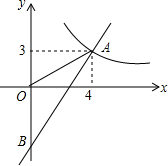 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com