
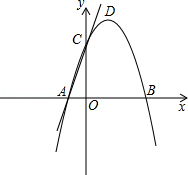
 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
 .请你计算这个“W”图案的高与宽的比到底是多少?
.请你计算这个“W”图案的高与宽的比到底是多少?科目:初中数学 来源:不详 题型:填空题
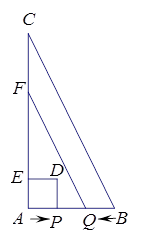
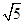 cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).
cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
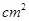 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x﹣2)2+1 | B.y=(x+2)2+1 | C.y=(x﹣2)2﹣3 | D.y=(x+2)2﹣3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
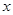 轴两交点间的距离为8,(1)试求该抛物线的关系式;
轴两交点间的距离为8,(1)试求该抛物线的关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
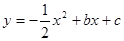 的图象经过这两点
的图象经过这两点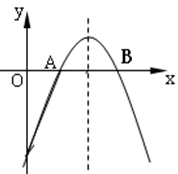
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
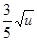 ,y2=
,y2=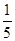 u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).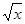 =t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
=t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com