
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=![]() AD,在Rt△ABC中,因为M是AC的中点,故BM=
AD,在Rt△ABC中,因为M是AC的中点,故BM=![]() AC,即可得到结论;
AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=![]() AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到
AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到![]() ,再由MN=BM=1,得到BN的长.
,再由MN=BM=1,得到BN的长.
试题解析:(1)在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,且MN=![]() AD,在Rt△ABC中,∵M是AC的中点,∴BM=
AD,在Rt△ABC中,∵M是AC的中点,∴BM=![]() AC,又∵AC=AD,∴MN=BM;
AC,又∵AC=AD,∴MN=BM;
(2)∵∠BAD=60°且AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)知,BM=![]() AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴
AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴![]() ,而由(1)知,MN=BM=
,而由(1)知,MN=BM=![]() AC=
AC=![]() ×2=1,∴BN=
×2=1,∴BN=![]() .
.


科目:初中数学 来源: 题型:
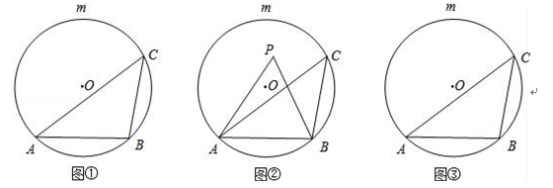
【题目】如图①,AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)若∠ACB=45°,点P是⊙O上一点(不与A、B重合),则∠APB= ;
(2)如图②,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:㎡),绘制了统计图,如图所示,下面有四个推断:
① 年用水量不超过180㎡的该市居民家庭按第一档水价交费
② 年用水量超过240㎡的该市居民家庭按第三档水价交费
③ 该市居民家庭年用水量的中位数在150-180之间
④ 该市居民家庭年用水量的平均数不超过180
正确的是( )
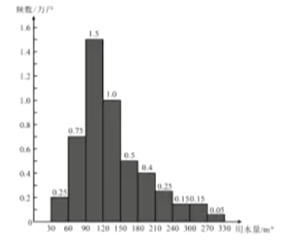
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
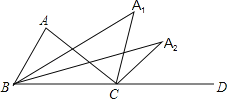
【题目】如图,△ABC中,∠A=96°,D是BC延长线上的一点,∠ABC与∠ACD(△ACB的外角)的平分线交于A1点,则∠A1=_______度;如果∠A=α,按以上的方法依次作出∠BA2C,∠BA3C…∠BAnC(n为正整数),则∠An=_______度(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
![]()
(1)甲队成绩的中位数是_______分,乙队成绩的众数是_______分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com