
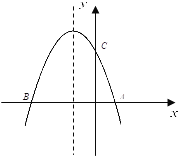
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)Q(-1,2).
;(2)Q(-1,2).
【解析】试题分析:(1)把A(1,0)B(-3,0)代入![]() 然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
试题解析:解(1)把A(1,0)B(-3,0)代入到
![]() 3分
3分
∴抛物线的解析式为y=-x2-2x+3 5分
(2)存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点,
设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入到

令XQ="-1" 得YQ=2 ∴Q(-1,2) 10分


科目:初中数学 来源: 题型:
【题目】综合实践:
问题情境
数学活动课上,老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图I,在正方形![]() 中,点
中,点![]() 为边
为边![]() 的中点.将
的中点.将![]() 以点
以点![]() 为旋转中心,顺时针方向旋转,当点
为旋转中心,顺时针方向旋转,当点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上时,连接
上时,连接![]() .
.
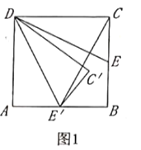
“兴趣小组”发现的结论是:![]() ;
;
“卓越小组”发现的结论是:![]() .
.
解决问题
(1)请你证明“兴趣小组”和“卓越小组”发现的结论;
拓展探究
证明完“兴趣小组”和“卓越小组”发现的结论后,“智慧小组”提出如下问题:如图2,连接![]() ,若正方形
,若正方形![]() 的边长为
的边长为![]() ,求出
,求出![]() 的长度.
的长度.
(2)请你帮助智慧小组写出线段![]() 的长度.(直接写出结论即可)
的长度.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
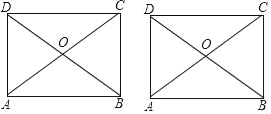
【题目】如图,已知矩形ABCD,AB=6,AD=2![]() ,对角线AC,BD交于点O,E为对角线AC上一点.
,对角线AC,BD交于点O,E为对角线AC上一点.
(1)求证:△OBC是等边三角形;
(2)连结BE,当BE=![]() 时,求线段AE的长;
时,求线段AE的长;
(3)在BC边上取点F,设P,Q分别为线段AE,BF的中点,连结EF,PQ.若EF=2,求PQ的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图1所示放置,其中点![]() 在
在![]() 边上,
边上,![]() ,斜边
,斜边![]() .将三角板
.将三角板![]() 绕点
绕点![]() 顺时针旋转,记旋转角为
顺时针旋转,记旋转角为![]() .
.
(1)在图1中,设![]() 与
与![]() 的交点为
的交点为![]() ,则线段AF的长为 ;
,则线段AF的长为 ;

(2)当![]() 时,三角板
时,三角板![]() 旋转到
旋转到![]() ,的位置(如图2所示),连接
,的位置(如图2所示),连接![]() ,请判断四边形
,请判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;

(3)当三角板![]() 旋转到
旋转到![]() 的位置(如图3所示)时,此时点
的位置(如图3所示)时,此时点![]() 恰好在
恰好在![]() 的延长线上.①求旋转角
的延长线上.①求旋转角![]() 的度数;②求线段
的度数;②求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
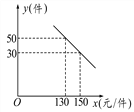
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )

A.8B.12C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com