
【题目】在阳光下,小东同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.
米.

![]() 同一时刻
同一时刻![]() 米的竹竿的影长为________米.
米的竹竿的影长为________米.
![]() 同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为
同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为![]() 米,第一级台阶的高为
米,第一级台阶的高为![]() 米,落在地面上的影子长为
米,落在地面上的影子长为![]() 米,则树的高度为________米.
米,则树的高度为________米.
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数的图象与x轴交于同一点,则称这两个函数为一对“x牵手函数”,这个交点为“x牵手点”.
(1)一次函数y=x﹣1与x轴的交点坐标为 ;一次函数y=ax+2与一次函数y=x﹣1为一对“x牵手函数”,则a= ;
(2)已知一对“x牵手函数”:y=ax+1与y=bx﹣1,其中a,b为一元二次方程x2﹣kx+k﹣4=0的两根,求它们的“x牵手点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.求:DP的长及点D的坐标.
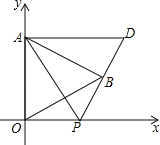
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .点
.点![]() 在函数图象上,
在函数图象上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
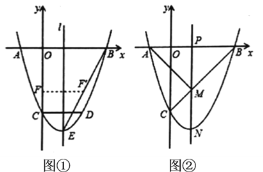
(1)求![]() 的值;
的值;
(2)如图①,连接![]() , 线段
, 线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点F'恰好在线段BE上,求点
的对称点F'恰好在线段BE上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:直线
.试问:直线![]() 右侧的抛物线上是否存在点
右侧的抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
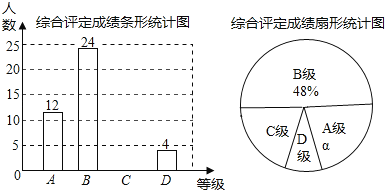
请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;a= %;C级对应的圆心角为 度.
(2)补全条形统计图;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com