
 如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )
如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )| A. | 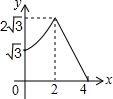 | B. | 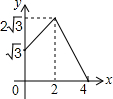 | C. | 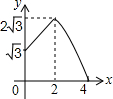 | D. | 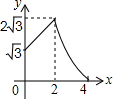 |
分析 先过A作AH⊥BC,求得AD和BC之间的距离,再分两种情况进行讨论,第一种是点Q在CE上移动,第二种是点Q在CP上移动,根据△BPQ面积的不同计算方式,分别列出函数关系式即可.
解答 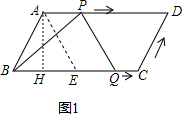 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
过A作AH⊥BC于H,则∠AHB=90°,
∵AB=2,∠ABC=60°,
∴AH=AB×sin60°=$\sqrt{3}$,即AD和BC之间的距离为$\sqrt{3}$,
∵BC=4,E为BC中点,
∴BE=CE=$\frac{1}{2}$BC=2.
①当Q在BC上时,如图1,
∵AD∥BC,AE∥PQ,
∴四边形AEQP是平行四边形,
∴AP=EQ=x,
∴S△BPQ=$\frac{1}{2}$×BQ×AH=$\frac{1}{2}$(2+x)×$\sqrt{3}$,
即y=$\frac{\sqrt{3}}{2}$x+$\sqrt{3}$(0≤x≤2);
②当Q在CD上时,如图2,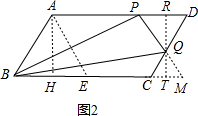
延长PQ交BC的延长线于M,过Q作RT⊥AD于R,交BC的延长线于T,
∵AD∥BC,
∴QT⊥CB,
即RT=AH=$\sqrt{3}$,
∵AD=BC=4,CE=BE=2,AP=EM=x,
∴DP=4-x,CM=x-2,
∵AD∥BC,
∴△PDQ∽△MCQ,
∴$\frac{RQ}{TQ}$=$\frac{DP}{CM}$,
∴$\frac{\sqrt{3}-QT}{QT}$=$\frac{4-x}{x-2}$,
解得:QT=$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$,
∴y=S△BPM-S△BQM
=$\frac{1}{2}$•(2+x)•$\sqrt{3}$-$\frac{1}{2}$•(2+x)•($\frac{\sqrt{3}}{2}$x-$\sqrt{3}$)
=-$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$(2<x≤4),
由①和②可知,函数图象为分段函数,当0≤x≤2时,函数图象是线段;当2<x≤4时,函数图象是开口向下的抛物线.
故选(C)
点评 本题主要考查了动点问题的函数图象,考核了学生分析问题、解决问题的能力.解题时需要运用平行四边形的性质与判定,以及相似三角形的判定与性质等,其关键是深刻理解动点移动时的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{4x+6y=3}\\{9x-6y=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+3y=9}\\{6x-2y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x+9y=3}\\{6x-4y=11}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
| 甲队 | 30 | n | 600 |
| 乙队 | m | n-14 | 1160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
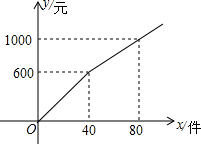 商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
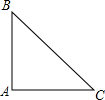 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com