
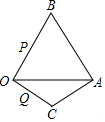
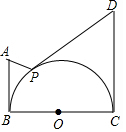
 ��֪���ȱߡ�OAB�ı߳�Ϊ3����һ������OCA���OAB�й�����OA����OC=AC����C=120�㣮����������P��Q�ֱ��B��O����ͬʱ��������P��ÿ��3����λ���ٶ���BO���O�˶�����Q��ÿ��1����λ���ٶ���OC���C�˶���������һ���㵽���յ�ʱ����һ����Ҳ�漴ֹͣ�˶�����ش��������⣺
��֪���ȱߡ�OAB�ı߳�Ϊ3����һ������OCA���OAB�й�����OA����OC=AC����C=120�㣮����������P��Q�ֱ��B��O����ͬʱ��������P��ÿ��3����λ���ٶ���BO���O�˶�����Q��ÿ��1����λ���ٶ���OC���C�˶���������һ���㵽���յ�ʱ����һ����Ҳ�漴ֹͣ�˶�����ش��������⣺���� ��1����������ֱ��ʾ��QO��OP�ij��������ó�S��t�Ĺ�ϵʽ��
��2�������OCDΪ���������Σ���ô��D��OA����OB���ϻ�AB�����������Σ�ÿһ�����Σ����п���OΪ���Ƕ��㣬CΪ���Ƕ��㣬DΪ���Ƕ��㣬�ֱ����ۣ��ó��𰸣�
��� �⣨1����ͼ1����OC=AC����ACO=120�㣬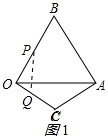
���AOC=��OAC=30�㣮
���POQ=90�㣬
��OQ=t��OP=3-3t��
��S��OPQ=$\frac{1}{2}$OQ•OP=$\frac{1}{2}$t•��3-3t��=-$\frac{3}{2}$t2+$\frac{3}{2}$t��
��S=-$\frac{3}{2}$t2+$\frac{3}{2}$t��
��2����ͼ2����i����D����OA�ϣ�
����DΪ���Ƕ���ʱ����OC�Ĵ�ֱƽ���߽�OA��D��
����OΪ���Ƕ���ʱ����OA�Ͻ�ȡOD=OC��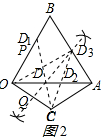
��ii����D����OB�ϣ�
���ڡ�BOC=90�㣬��˲�������C��DΪ����ĵ��������Σ�
��OD=OC����OB�Ͻ�ȡOD=OC��
��iii����D����AB��ʱ��
��ʱOD����̾���ΪOD��ABʱ����ʱOD��OC����������OΪ����ĵ��������Σ�
����CΪ����ʱ��D���A���غϣ�
����DΪ����ʱ��OD=CD����OC�Ĵ�ֱƽ���߽�AB��D��
���������������ĵ�D����4����
�ʴ�Ϊ��4��
���� �������������ۺ���Ŀ�������˵��������ε��ж����ȱ������ε����ʡ�ȫ�������ε��ж������ʡ�ֱ�������������֪ʶ���ó���OCDΪ����������ʱ��ע��������ۣ��������ظ�������©��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
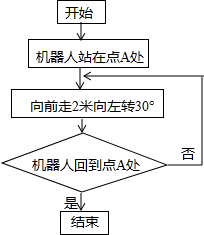 �Ƽ���Ϊij�����˱���һ�γ��������������ƽ���ϰ���ͼ����ʾ�IJ������ߣ���ô�û��������ߵ���·��Ϊ��������
�Ƽ���Ϊij�����˱���һ�γ��������������ƽ���ϰ���ͼ����ʾ�IJ������ߣ���ô�û��������ߵ���·��Ϊ��������| A�� | 12�� | B�� | 16�� | C�� | 24�� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1����֪����x��һԪ���η��̣�a+c��x2+bx+��a-c��=0������a��b��c�ֱ�Ϊ��ABC�ı߳�������a��b����c�ֱ�Ϊ��M��Բ������Ͱ뾶����ơ�MΪ��ABC�ġ�����Բ����
��1����֪����x��һԪ���η��̣�a+c��x2+bx+��a-c��=0������a��b��c�ֱ�Ϊ��ABC�ı߳�������a��b����c�ֱ�Ϊ��M��Բ������Ͱ뾶����ơ�MΪ��ABC�ġ�����Բ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����Rt��ABC�У���A=90�㣬BDƽ�֡�ABC����C��BD�Ĵ���CE����֤��BD=2CE��
��ͼ����֪����Rt��ABC�У���A=90�㣬BDƽ�֡�ABC����C��BD�Ĵ���CE����֤��BD=2CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com