
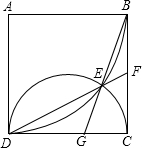
 如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径的弧与以DC为直径的半圆交于点E,连接DE并延长交BC于F,连接BE并延长交DC于G.
如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径的弧与以DC为直径的半圆交于点E,连接DE并延长交BC于F,连接BE并延长交DC于G.分析 (1)作辅助线,构建直角三角形和平行线,先根据切割线定理得出BF=FC,由勾股定理和面积法依次求出EC、EF、DE的长,根据同角的三角函数相等列式求FH的长,即可得到BH的长,根据平行线分线段成比例定理求出CG和DG的长,计算比值即可;
(2)根据同高两三角形面积的关系分别求出△EFC和△EGC的面积,求和即可.
解答 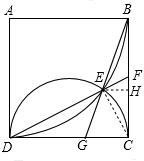 解:(1)如图,过E作EH⊥BC于H,连接CE,
解:(1)如图,过E作EH⊥BC于H,连接CE,
∵$\widehat{BD}$是以A为圆心,以AB为半径的弧,且四边形ABCD是正方形,
∴BF为⊙A的切线,
∴BF2=EF•DF,
同理:CF是半圆$\widehat{DC}$的切线,
∴CF2=EF•DF,
∴BF=CF=$\frac{1}{2}$BC=$\frac{1}{2}$,
由勾股定理得:DF=$\sqrt{D{C}^{2}+C{F}^{2}}$=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
∵S△DCF=$\frac{1}{2}$DC•CF=$\frac{1}{2}$DF•EC,
∴1×$\frac{1}{2}$=$\frac{\sqrt{5}}{2}$EC,
∴EC=$\frac{\sqrt{5}}{5}$,
由勾股定理得:EF=$\sqrt{F{C}^{2}-E{C}^{2}}$=$\sqrt{(\frac{1}{2})^{2}-(\frac{\sqrt{5}}{5})^{2}}$=$\frac{\sqrt{5}}{10}$,
DE=DF-EF=$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{5}}{10}$=$\frac{2\sqrt{5}}{5}$,
∵EH⊥BC,DC⊥BC,
∴EH∥DC,
∴$\frac{EF}{DF}=\frac{EH}{DC}$
∴$\frac{\frac{\sqrt{5}}{10}}{\frac{\sqrt{5}}{2}}$=$\frac{EH}{1}$,
∴EH=$\frac{1}{5}$,
tan∠FEH=tan∠FDC=$\frac{FC}{DC}=\frac{FH}{EH}$,
∴$\frac{FH}{EH}=\frac{1}{2}$,
∴FH=$\frac{1}{10}$,
∵EH∥GC
∴$\frac{EH}{CG}=\frac{BH}{BC}$,
∴$\frac{\frac{1}{5}}{CG}=\frac{\frac{1}{2}+\frac{1}{10}}{1}$,
∴CG=$\frac{1}{3}$,
∴DG=CD-CG=1-$\frac{1}{3}$=$\frac{2}{3}$,
∴DG:CG=$\frac{2}{3}$:$\frac{1}{3}$=2:1;
(2)∵$\frac{EF}{DE}$=$\frac{1}{4}$,
∴$\frac{{S}_{△EFC}}{{S}_{△DCE}}$=$\frac{1}{4}$,
∴S△EFC=$\frac{1}{5}$S△DCF=$\frac{1}{5}$×$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{20}$,
S△DEC=$\frac{1}{20}$×4=$\frac{1}{5}$,
∵DG:CG=2:1,
∴$\frac{{S}_{△DGE}}{{S}_{△EGC}}$=$\frac{2}{1}$,
∴S△EGC=$\frac{1}{3}$S△DEC=$\frac{1}{3}$×$\frac{1}{5}$=$\frac{1}{15}$,
∴S四边形EFCG=S△EFC+S△EGC=$\frac{1}{20}$+$\frac{1}{15}$=$\frac{7}{60}$.
点评 本题考查了正方形、圆及圆的切线的性质,运用了切割线定理证明线段相等;本题计算量大,比较麻烦;再求线段比和面积比时,可分别利用平行线分线段成比例定理和勾股定理求线段的长;再求面积比时,常运用同高两三角形面积的比就是对应底边的比.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,△>0 | B. | a<0,△>0 | C. | a>0,△<0 | D. | a<0,△<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com