某厂生产某种零件,该厂为鼓励销售商订货,提供了如下信息:
①每个零件的成本价为40元;
②若订购量在100个以内,出厂价为60元;若订购量超过100个时,每多订1个,订购的全部零件的出厂单价就降低0.02元;
③实际出厂单价不能低于51元.
根据以上信息,解答下列问题:
(1)当一次订购量为______个时,零件的实际出厂单价降为51元.
(2)设一次订购量为x个时,零件的实际出厂单价为P元,写出P与x的函数表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂价-成本).
解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为x个,则x=100+
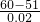
=550
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元.
故答案为:550;
(2)当0<x≤100时,P=60
当100<x<550时,P=60-0.02(x-100)=62-
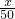
当x≥550时,P=51
所以P=
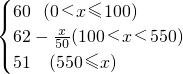
;
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(P-40)x=

当x=500时,L=22×500-
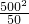
=6000(元);当x=1000时,L=(51-40)×1000=11000(元),
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.
分析:(1)由题意设每个零件的实际出厂价恰好降为51元时,一次订购量为x个,则x=100+
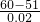
=550进而得出答案;
(2)前100件单价为P,当进货件数大于等于550件时,P=51,则当100<x<550时,P=60-0.02(x-100)=62-
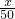
得到P为分段函数,写出解析式即可;
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,表示出L与x的函数关系式,然后令x=500,1000即可得到对应的利润.
点评:本小题主要考查了二次函数的应用以及分段函数的应用,注意利用自变量取值范围得出函数解析式是解题关键.

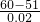 =550
=550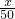
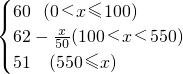 ;
;
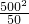 =6000(元);当x=1000时,L=(51-40)×1000=11000(元),
=6000(元);当x=1000时,L=(51-40)×1000=11000(元),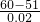 =550进而得出答案;
=550进而得出答案;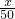 得到P为分段函数,写出解析式即可;
得到P为分段函数,写出解析式即可;


