
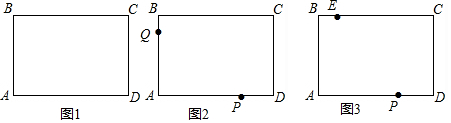
分析 (1)由条件可求得AB=4,BC=6,由勾股定理可求出BD的长;
(2)根据题意得出BQ=x,PD=2x,AQ=4-x,AP=6-2x,△CPQ的面积S=矩形ABCD的面积-△APQ的面积-△CDP的面积-△BCQ的面积,即可得出结果;
(3)求出CE=6-1=5,分三种情况:
①当CP=CE=5时,作EM⊥AD于M,则AM=EB=1,EM=AB=4,由勾股定理求出PD,得出PM,再由勾股定理求出PE,即可得出△EPC的周长;
②当PE=CE=5时,同①得:△EPC的周长=10+2$\sqrt{5}$;
③当PC=PE时,作PN⊥BC于N,则PN=CD=4,EN=CN=$\frac{1}{2}$CE=2.5,由勾股定理得出PE=PC=$\frac{\sqrt{89}}{2}$,求出△EPC的周长,即可得出结论.
解答 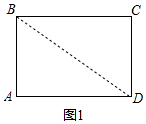 解:(1)连接BD,如图1所示,
解:(1)连接BD,如图1所示,
∵$\sqrt{AB-4}$+|BC-6|=0,
∴AB=4,BC=6,
∴AD=BC=6,
在Rt△ABD中,由勾股定理可求得BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$(cm);
(2)连接CQ、PQ、CP,如图2所示,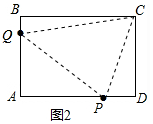
根据题意得:BQ=x,PD=2x,AQ=4-x,AP=6-2x
△CPQ的面积S=矩形ABCD的面积-△APQ的面积-△CDP的面积-△BCQ的面积
=6×4-$\frac{1}{2}$×(6-2x)(4-x)-$\frac{1}{2}$×2x×4-$\frac{1}{2}$×6×x
=12-x2(cm2);
(3)∵BC=6,EB=1,
∴CE=6-1=5,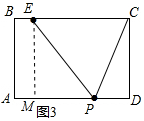
分三种情况:
①当CP=CE=5时,作EM⊥AD于M,如图3所示,
则AM=EB=1,EM=AB=4,
∵∠D=90°,CD=AB=4,
∴PD=$\sqrt{C{P}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴PM=AD-AM-PD=6-1-3=2,
∴PE=$\sqrt{E{M}^{2}+P{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,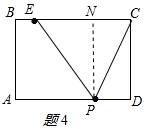
∴△EPC的周长=CE+CP+PE=10+2$\sqrt{5}$(cm);
②当PE=CE=5时,同①得:△EPC的周长=10+2$\sqrt{5}$(cm);
③当PC=PE时,作PN⊥BC于N,如图4所示,
则PN=CD=4,EN=CN=$\frac{1}{2}$CE=2.5,
∴PE=PC=$\sqrt{P{N}^{2}+C{N}^{2}}$=$\sqrt{{4}^{2}+2.{5}^{2}}$=$\frac{\sqrt{89}}{2}$,
∴△EPC的周长=CE+PC+PE=5+$\sqrt{89}$(cm);
综上所述:△EPC的周长为(10+2$\sqrt{5}$)cm或(5+$\sqrt{89}$)cm.
点评 本题是三角形综合题目,考查了勾股定理、矩形的性质、三角形面积和周长的计算等知识;本题综合性强,有一定难度,特别是(3)中,需要运用勾股定理进行计算和进行分类讨论才能得出结果.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
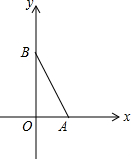 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com