(1)解:
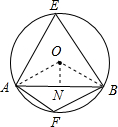
过O作ON⊥AB于N,连接OA、OB,
由垂径定理得:AN=BN=

AB=3

,
∵在Rt△ONB中,cos∠OBN=
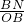
=

,
∴∠OBN=30°,∠BON=90°-30°=60°,
∵OA=OB,ON⊥AB,
∴∠AOB=2∠BON=120°,
由圆周角定理得:①∠AEB=

∠AOB=60°,
②∠AFB=180°-60°=120°,
答:弦AB所对的圆周角是60°或120°.
(2)解:分为两种情况:
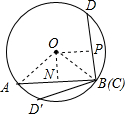
过O作OP⊥CD于P,
由垂径定理得:BP=DP=3

,
∵在Rt△BPO中,cos∠PBO=
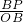
=

,
∴∠PBO=45°,
由(1)知:∠OBN=30°,
∴∠ABD=45°+30°=75°;
当D在D′时,∠ABD=45°-30°=15°;
即∠ABD的度数是15°或75°.
连接OC,OD,OP,
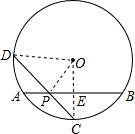
∵C是弧AB的中点,
∴OC⊥AB,
∵AB=6

,半径为6,
∴BE=AE=3

,
由勾股定理得:OE=3,
∴CE=6-3=3=OC,
∴AB垂直平分OC,
∴OP=PC,
即△OPC是等腰三角形,且OP=PC;
∵CD=6

,OC=OD=6,
∴OC
2+OD
2=CD
2,
△COD为等腰直角三角形,
∴∠PCO=45°,
∵△PCO为等腰三角形,
∴∠POC=∠PCO=45°,
∴∠OPC=90°,
即OP⊥CD,
∴在等腰直角△OCD中,DP=CP,
∴CP=

CD=3

,
∴OP=CP=3

答:∠ABD的度数是15°或75°,OP的长是3

.
分析:(1)过O作ON⊥AB于N,连接OA、OB,由垂径定理求出AN=BN=3

,根据cos∠OBN=

,求出∠OBN、∠BON,求出∠AOB,根据圆周角定理求出∠AEB和∠AFB即可;
(2)过O作OP⊥CD于P,由垂径定理求出BP=DP,根据cos∠PBO求出∠PBO=45°,由(1)知:∠OBN=30°,代入求出即可;连接OC,OD,OP,求出BE=AE=3

,由勾股定理求出OE=3,得出AB垂直平分OC,推出△OPC是等腰三角形,求出△COD为等腰直角三角形,推出∠PCO=45°,求出∠OPC=90°即可.
点评:本题综合考查了锐角三角函数定义,勾股定理及逆定理,直角三角形斜边上中线性质,垂径定理,圆周角定理等知识点的应用,主要考查学生运用这些性质进行推理和计算的能力,注意:每一步都要进行分类讨论啊.

 如图,在半径为6的⊙O中,弦AB的长为
如图,在半径为6的⊙O中,弦AB的长为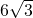 ,
,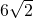 的弦CD在圆周上运动,当点C与B重合时,求∠ABD的度数;当点C是
的弦CD在圆周上运动,当点C与B重合时,求∠ABD的度数;当点C是 的中点时,设CD与AB交于点P,求OP的长.
的中点时,设CD与AB交于点P,求OP的长.
 AB=3
AB=3 ,
,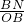 =
= ,
, ∠AOB=60°,
∠AOB=60°,
 ,
,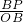 =
= ,
,
 ,半径为6,
,半径为6, ,
, ,OC=OD=6,
,OC=OD=6, CD=3
CD=3 ,
,
 .
. ,根据cos∠OBN=
,根据cos∠OBN= ,求出∠OBN、∠BON,求出∠AOB,根据圆周角定理求出∠AEB和∠AFB即可;
,求出∠OBN、∠BON,求出∠AOB,根据圆周角定理求出∠AEB和∠AFB即可; ,由勾股定理求出OE=3,得出AB垂直平分OC,推出△OPC是等腰三角形,求出△COD为等腰直角三角形,推出∠PCO=45°,求出∠OPC=90°即可.
,由勾股定理求出OE=3,得出AB垂直平分OC,推出△OPC是等腰三角形,求出△COD为等腰直角三角形,推出∠PCO=45°,求出∠OPC=90°即可.

 阅读快车系列答案
阅读快车系列答案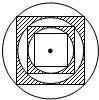 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )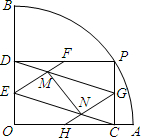 (2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是
(2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是