
分析 由以[x]表示不大于x的最大整数,可设x的整数部分为m,小数部分为n,即可得x=m+n,然后分别从当0≤n<$\frac{1}{3}$时,当$\frac{1}{3}$≤n<$\frac{1}{2}$时,当$\frac{1}{2}$≤n<$\frac{2}{3}$时,当$\frac{2}{3}$≤n<1时去分析求解,即可求得答案.
解答 解:设x的整数部分为m,小数部分为n,
∴x=m+n,
当0≤n<$\frac{1}{3}$时,
方程[2x]+[3x]=95为:5m=95,
解得:m=19,
∴x=19+n,(0≤n<$\frac{1}{3}$)
当$\frac{1}{3}$≤n<$\frac{1}{2}$时,方程[2x]+[3x]=95为:2m+3m+1=95,即m=$\frac{94}{5}$不为整数,不合题意,
当$\frac{1}{2}$≤n<$\frac{2}{3}$时,2m+1+3m+1=95,即m=$\frac{93}{5}$不为整数,不合题意,
当$\frac{2}{3}$≤n<1时,2m+1+3m+2=95,m=$\frac{92}{5}$不为整数,不合题意,
∴方程[2x]+[3x]=95的解为:19≤x<$\frac{58}{3}$.
点评 此题考查了取整函数的知识.此题难度较大,解题的关键是理解是取整函数的意义,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,∠ADC=90°,点E为边BC上的一点,连接DE,点F为ED上的一点,连接AF、BF,且AB=AC,AD=AF,∠BAC=∠DAF.
如图,四边形ABCD中,∠ADC=90°,点E为边BC上的一点,连接DE,点F为ED上的一点,连接AF、BF,且AB=AC,AD=AF,∠BAC=∠DAF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
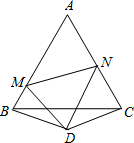 如图,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N,连接MN.求△AMN的周长.
如图,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N,连接MN.求△AMN的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
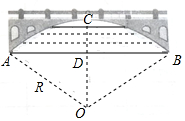 赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,求桥弧AB所在圆的半径.
赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,求桥弧AB所在圆的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 已知a=b,则a2=b2 | B. | 已知a=b,m为任意有理数,则ma=mb | ||
| C. | 已知ma=mb,m为任意有理数,则a=b | D. | 已知ax=b,且a≠0,则x=$\frac{b}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com