
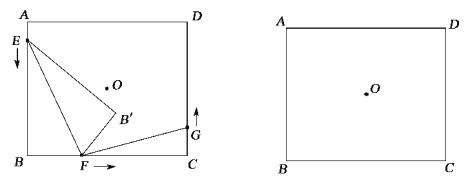
【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB'为正方形;
(2)当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)2.5;(2)3或4;(3)不存在,理由见解析
【解析】
(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;
(2)分两种情况讨论,①△EBF≌△FCG,②△EBF≌△GCF,分别根据对应边相等列等式计算即可;
(3)本问为存在型问题.假设存在,则可以分别求出在同一条件下的t值,但它们互相矛盾,所以不存在.
解:(1)若四边形EBFB′为正方形,则BE=BF,BE=10-t,BF=3t,
即:10-t=3t,
解得t=2.5;
(2)分两种情况讨论:
①△EBF≌△FCG,
则EB=FC,BF=CG,
∴![]() ,
,
解得:![]() ,
,
②当△EBF≌△GCF时,
则EB=GC,BF=FC,
∴![]() ,
,
解得:![]() ,
,
综上,当x=3或4时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等;
(3)假设存在实数t,使得点B′与点O重合.
如图,过点O作OM⊥BC于点M, ON⊥AB于点N,
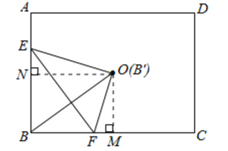
则在Rt△OFM中![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]()
在Rt△OEN中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴假设不成立,
即不存在实数t,使得点B'与点O重合.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】阅读下述材料:
我们在学习二次根式时,熟悉的分母有理化以及应用.其实,有一个类似的方法叫做“分子有理化”:
与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式比如:

分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:
比较![]() 和
和![]() 的大小.可以先将它们分子有理化如下:
的大小.可以先将它们分子有理化如下:
![]()
![]()
因为![]() ,所以
,所以![]()
再例如:求![]() 的最大值.做法如下:
的最大值.做法如下:
解:由![]() 可知
可知![]() ,而
,而![]()
当![]() 时,分母
时,分母![]() 有最小值2,所以的最大值是2.
有最小值2,所以的最大值是2.
解决下述问题:
(1)比较![]() 和
和![]() 的大小;
的大小;
(2)求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60方向,距离灯塔100海里的A处,它计划去往位于灯塔P的北偏东45方向上的B处.(参考数据![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知水池中有800立方米的水,每小时抽50立方米.
(1)写出剩余水的体积![]() 立方米与时间
立方米与时间![]() (时)之间的函数关系式.
(时)之间的函数关系式.
(2)写出自变量![]() 的取值范围.
的取值范围.
(3)10小时后,池中还有多少水?
(4)几小时后,池中还有100立方米的水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:

(1)请将下表补充完整:

(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab2+2ab+a.如:13=1×32+2×1×3+1=16
(1)求2(-1)的值;
(2)若(a+1)3=32,求a的值;
(3)若m=2x,n=(![]() x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com