
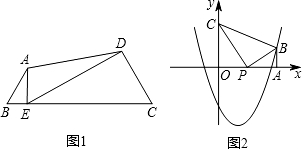
分析 (1)先确定出点B的横坐标,代入二次函数解析式中,求出点B的纵坐标,即可;
(2)用两角相等的两三角形相似即可;
(3)①由△OCP∽△APB和△ABP∽△PCB,得到两个方程求解,②由△OCP∽△APB和△ABP∽△PBC,得到两个方程求解.
解答 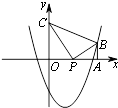 解:(1)∵过点A(6,0)作x轴的垂线交二次函数y=$\frac{1}{2}$x2-2x-4的图象于点B,
解:(1)∵过点A(6,0)作x轴的垂线交二次函数y=$\frac{1}{2}$x2-2x-4的图象于点B,
∴把x=6代入二次函数解析式中,得y=$\frac{1}{2}$×62-2×6-4=2,
∴B点的坐标为(6,2).
(2)由题意得,∠BAP=∠COP=90°.
∵PC⊥PB,
∴∠BPC=90°.
∴∠CPO+∠APB=90°.
∵∠CPO+∠OCP=90°,
∴∠OCP=∠APB.
∴△OCP∽△APB.
∴由定义可得,点P是四边形ABCO在边OA 上的相似点.
(3)设点P(m,0),C(0,a)
∵A(6,0),B(6,2),
∴AP=6-m,OP=m,AB=2,OC=a,PC=$\sqrt{{m}^{2}+{a}^{2}}$,PB=$\sqrt{(m-6)^{2}+4}$,
由(2)有,△OCP∽△APB,
∴$\frac{OC}{AP}=\frac{OP}{AB}=\frac{CP}{PB}$,
∴$\frac{a}{6-m}=\frac{m}{2}$①,
①当△ABP∽△PCB时,
∴$\frac{AP}{PB}=\frac{AB}{PC}$,
∴$\frac{6-m}{\sqrt{(m-6)^{2}+4}}=\frac{2}{\sqrt{{m}^{2}+{a}^{2}}}$②
联立①②得,a=2或a=-2(舍),
当a=2时,$\frac{2}{6-m}=\frac{m}{2}$,
∴m=3±$\sqrt{5}$,
∴P(3+$\sqrt{5}$,0)或P(3-$\sqrt{5}$,0),
②当△ABP∽△PBC时,
∴$\frac{AB}{PB}=\frac{AP}{PC}$,
∴$\frac{2}{\sqrt{(m-6)+4}}=\frac{6-m}{\sqrt{{m}^{2}+{a}^{2}}}$③,
联立①③得,m2=2a,
由①得到,m(6-m)=2a=m2
∴m=3或m=0(舍)
∴P(3,0).
即:点P的坐标为(3,0),(3+$\sqrt{5}$,0),(3-$\sqrt{5}$,0).
点评 此题是二次函数综合题,主要考查了待定系数法,相似三角形的性质和判定,新定义,解本题的关键是理解新定义,难点是求点P的坐标.


科目:初中数学 来源: 题型:选择题
| A. | -1-$\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | 1-$\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 40 | B. | 42 | C. | 46 | D. | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com