
【题目】如图1,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.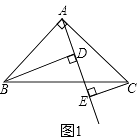
(1)求证:BD=DE+CE;
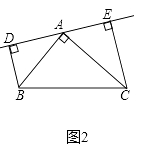
(2)若直线AE绕A点旋转到图2位置时(BD<CE),其余条件不变,则BD与DE、CE的数量关系如何?请予以证明;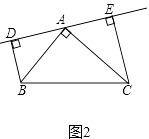
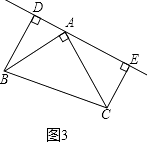
(3)若直线AE绕A点旋转到图3位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不需说明理由;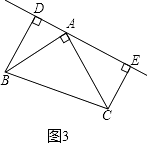
(4)根据以上的讨论,请用简洁的语言表述BD与DE、CE的数量关系.
【答案】
(1)
证明:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
在△ABD与△CAE中,
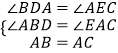 ,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=AD+DE=CE+DE,
∴BD=DE+CE
(2)
证明:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
在△ABD与△CAE中,
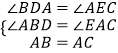 ,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵DE=AD+AE=CE+BD,
∴DE=BD+CE
(3)
证明:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
在△ABD与△CAE中,
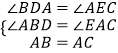 ,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵DE=AD+AE=BD+CE,
∴DE=BD+CE
(4)
证明:BD与CE的和等于DE或BD等于DE与CE的和
【解析】(1)证明△ABD≌△CAE,即可证得BD=AE,AD=CE,而AE=AD+DE=CE+DE,即可证得;(2)(3)图形变换了,但是(1)中的全等关系并没有改变,因而BD与DE、CE的关系并没有改变;(4)把BD与DE、CE的关系用语言表述出来即可.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度![]() (微克/毫升)与服药时间
(微克/毫升)与服药时间![]() 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当![]() 时,
时,![]() 与
与![]() 成反比).
成反比).

(1)根据图象分别求出血液中药物浓度上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对正方形的描述错误的是( )
A. 正方形的四个角都是直角 B. 正方形的对角线互相垂直
C. 邻边相等的矩形是正方形 D. 对角线相等的平行四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b中,k<0,b<0,则函数不经过下列选项中的那个象限( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1:y1=x1+2和直线l2:y2=﹣x2+4相交于点A,分别于x轴相交于点B和点C,分别与y轴相交于点D和点E.
(1)在平面直角坐标系中按照列表、描点、连线的方法画出直线l1和l2的图象,并写出A点的坐标.
(2)求△ABC的面积.
(3)求四边形ADOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com