
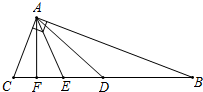
 如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )
如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )| A. | 4组 | B. | 5组 | C. | 6组 | D. | 7组 |
分析 根据三角形的角平分线、中线、高的概念进行解答.
解答 解:∵AD是Rt△ABC斜边BC上的中线,则BD=CD=AD=$\frac{1}{2}$BC.
∴∠C=∠DAC,∠B=∠DAB.
∵AE是△ABC中∠BAC的角平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
∴∠DAE=∠FAE.
∵AF是Rt△ABC斜边BC上的高线,
∴∠C=∠BAF,∠B=∠CAF,
∴∠C=∠DAC=∠BAF,∠B=∠DAB=∠CAF,∠DAE=∠FAE.
综上所述,图中相等的锐角共有7组,
故选:D.
点评 此题考查了三角形的角平分线、中线和高,是一道基础题,能够根据三角形的中线、角平分线和高的概念得到线段、角之间的关系.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:等边△ABC,边长为8cm,点D从C点出发沿BC方向以1cm/s速度运动,点P从A点出发沿AC方向以2cm/s速度运动,DE∥AC交AB于点E,点D、点P两点同时出发,设运动时间为t s,问:
已知:等边△ABC,边长为8cm,点D从C点出发沿BC方向以1cm/s速度运动,点P从A点出发沿AC方向以2cm/s速度运动,DE∥AC交AB于点E,点D、点P两点同时出发,设运动时间为t s,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
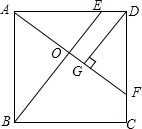 如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com