
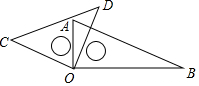
 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA与∠DOA互余 | D. | ∠AOD与∠COB互补 |
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
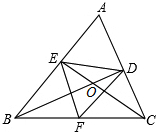 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随机事件发生的概率为$\frac{1}{2}$ | |
| B. | 天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 | |
| C. | 某福利彩票中奖率是1‰,意思是买这种彩票1000张,一定会中奖 | |
| D. | 通过抛一枚均匀硬币定谁先发球的比赛规则是公平的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com