
分析 根据题意可知点C在x轴上或者在y轴上,通过画图分析,符合要求的有四种情况,根据AC+BC=10,可以确定点C的坐标.
解答  解:∵点A(-4,0),B(4,0),点C在坐标轴上,且AC+BC=10,
解:∵点A(-4,0),B(4,0),点C在坐标轴上,且AC+BC=10,
∴点C所在的位置有四种情况:
第一种情况:点C在点A的左侧.
设点C的坐标为(x,0).
∵AC+BC=10,点A(-4,0),B(4,0),
∴(-4-x)+(4-x)=10.
解得,x=-5.
∴点C的坐标为(-5,0);
第二种情况:点C在点B的右侧.
设点C的坐标为(x,0).
∵AC+BC=10,
∴[x-(-4)]+(x-4)=10.
解得,x=5.
∴点C的坐标为(5,0);
第三种情况:点C在y轴上方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-4,0),B(4,0),
∴AC=BC=5,42+y2=52.
解得,y=±3.
∵点C在y轴上方,
∴点C的坐标为(0,3).
第四种情况:点C在y轴下方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-4,0),B(4,0),
∴AC=BC=5,42+y2=52.
解得,y=±3.
∵点C在y轴下方,
∴点C的坐标为(0,-3).
故答案为:(-5,0),(5,0),(0,3),(0,-3).
点评 本题考查的是勾股定理及坐标与图形的关系,关键是可以根据题目中的信息把点C的几种可能性都考虑到,画出相应的图形.


科目:初中数学 来源: 题型:选择题
 为减少雾霾天气,我们崇尚低碳生活,现有一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和”崇“相对的面上写的汉字是( )
为减少雾霾天气,我们崇尚低碳生活,现有一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和”崇“相对的面上写的汉字是( )| A. | 低 | B. | 碳 | C. | 生 | D. | 活 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)-2=4 | B. | 20×2-3=-$\frac{1}{8}$ | C. | 46÷(-2)6=64 | D. | $\sqrt{6}$-$\sqrt{2}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小东根据学习一次函数的经验,对函数y=|2x-1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
小东根据学习一次函数的经验,对函数y=|2x-1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
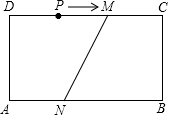 如图,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.点P在CD边上.
如图,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.点P在CD边上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
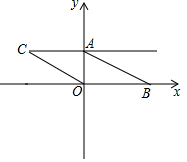 如图.已知在平面直角坐标系中.点A(0,m),点B(n,0),D(2m,n),且m、n满足(m-2)2+$\sqrt{n-4}$=0,将线段AB向左平移,使点B与点O重合,点C与点A对应.
如图.已知在平面直角坐标系中.点A(0,m),点B(n,0),D(2m,n),且m、n满足(m-2)2+$\sqrt{n-4}$=0,将线段AB向左平移,使点B与点O重合,点C与点A对应.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
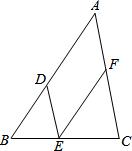 请在下列括号里填上合适的理由:
请在下列括号里填上合适的理由:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com