
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
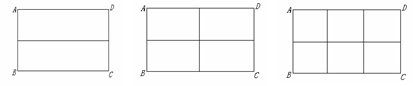 |
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6米,当AB为1米,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6米,设AB为![]() 米,长方形框架ABCD的面积为S= (用含
米,长方形框架ABCD的面积为S= (用含![]() 的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为米, 设AB为![]() 米,当AB是多少米时, 长方形框架ABCD的面积S最大.
米,当AB是多少米时, 长方形框架ABCD的面积S最大.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
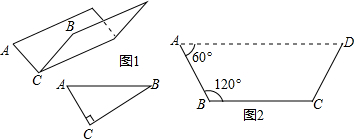
 初三(1)班数学兴趣小组,用高为1.2米的测倾器、皮尺测量校内一办公楼的高AB时,设计如图所示的测量方案(测点E、F与楼底B在同一直线上),并有四个同学分别测量出以下四组数据(角的度数、线段的长):
初三(1)班数学兴趣小组,用高为1.2米的测倾器、皮尺测量校内一办公楼的高AB时,设计如图所示的测量方案(测点E、F与楼底B在同一直线上),并有四个同学分别测量出以下四组数据(角的度数、线段的长):查看答案和解析>>
科目:初中数学 来源: 题型:
| 81 |
| 2 |
| 81 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 我校初三(11)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:
我校初三(11)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com