Question

18．如图，已知直线y=3x+3与x轴交于点A，与y轴交于点C，过点C的直线y=-x+b与x轴交于点B．
（1）b的值为3；
（2）若点D的坐标为（0，-1），将△BCD沿直线BC对折后，点D落到第一象限的点E处，求证：四边形ABEC是平行四边形；
（3）在直线BC上是否存在点P，使得以P、A、D、B为顶点的四边形是平行四边形？如果存在，请求出点P的坐标；如果不存在，请说明理由．

Answer 1

分析 （1）先由点C在直线y=3x+3上，求出点C坐标，代入直线y=-x+b中即可．
（2）先求出∠OBC=∠OCB=45°，进而判断出CE∥AB，最后判断出CE=AB 即可；
（3）方法①先确定出直线AD，BC解析式，进而判断出AD∥BC，使得以P、A、D、B为顶点的四边形是平行四边形，只要AD=PB即可．
方法②，分两种情况，先用平移的性质得出得出直线的解析式，求出满足平行四边形的交点坐标，最后判断此点在直线BC上，即可得出点P坐标．

解答 （1）∵直线y=3x+3与x轴交于点A，与y轴交于点C，
∴C（0，3），
∵过点C的直线y=-x+b与x轴交于点B，
∴b=3，
故答案为3，
（2）证明：当b=3时，直线BC为y=-x+3
由x=0得，y=3，
∴C（0，3），OC=3
由y=0得，x=3，
∴B（3，0），OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45° 
由折叠得：∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB 
由y=3x+3，令y=0得，x=-1，
∴A（-1，0）
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形．
（3）解：存在点P，使以P、A、D、B为顶点的四边形是平行四边形．
方法①如图，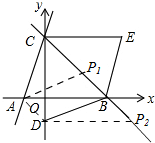

∵A（-1，0）、D（0，-1），
∴直线AD解析式为y=-x-1，
∵B（3，0），C（0，3），
∴直线BC解析式为y=-x+3．
∴AD∥BC，
∵点P在直线BC上，
∴设点P坐标为（m，-m+3），
∴PB²=（m-3）²+（-m+3）²，
∵使得以P、A、D、B为顶点的四边形是平行四边形，
∴PB=AD，
∴PB²=AD²，
∵AD²=2，
∴（m-3）²+（-m+3）²=2．
∴m₁=2，m₂=4，
∴P（2，1）或P（4，-1），
综上所述，存在点P，使以P、A、D、B为顶点的四边形是平行四边形．点P的坐标为P₁（2，1）或P₂（4，-1）．
方法②∵A（-1，0）、D（0，-1），
∴直线AD解析式为y=-x-1，
∵B（3，0），
∴过点B的直线l∥AD，直线l解析式为y=-x+3，
∴D（0，-1），
∴过点D的直线l'∥AB，直线l'的解析式为y=-1，
∴直线l和l'的交点坐标为M（4，-1），
∵直线BC解析式为y=-x+3．
∴点M在直线BC上，即点M就是所找的点P，
∴P（4，-1），
∵D（0，-1），B（3，0），
∴直线BD的解析式为y=$\frac{1}{3}$x-1，
∴过点A的直线a∥BD，直线a的解析式为y=$\frac{1}{3}$x+$\frac{1}{3}$，
∵直线l解析式为y=-x+3，
∴直线l和直线a的交点坐标为N（2，1），
∵直线BC解析式为y=-x+3．
∴点N在直线BC上，即点N就是所找的点P，
∴P（2，1），
综上所述，存在点P，使以P、A、D、B为顶点的四边形是平行四边形．点P的坐标为P₁（2，1）或P₂（4，-1）．

点评 此题是一次函数综合题，主要考查了坐标轴上点的特点，待定系数法求函数解析式，平行四边形的判定和性质，解本题的关键是四边形ABEC为平行四边形，判断出AD∥BC是解本题的难点．