
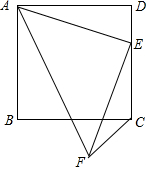
 正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E顺时针旋转90°得到EF,连接AF,FC,则FC=$\sqrt{2}$.
正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E顺时针旋转90°得到EF,连接AF,FC,则FC=$\sqrt{2}$. 分析 作FH⊥CD于H,如图,利用正方形的性质得DA=CD,∠D=90°,再根据旋转的性质得EA=EF,∠AEF=90°,接着证明△ADE≌△EHF得到DE=FH=1,AD=EH,所以EH=DC,则DE=CH=1,然后利用勾股定理计算FC的长.
解答 解:作FH⊥CD于H,如图,
∵四边形ABCD为正方形,
∴DA=CD,∠D=90°,
∵AE绕点E顺时针旋转90°得到EF,
∴EA=EF,∠AEF=90°,
∵∠DAE+∠AED=90°,∠FEH+∠AED=90°,
∴∠EAD=∠FEH,
在△ADE和△EHF中
$\left\{\begin{array}{l}{∠D=∠FHE}\\{∠EAD=∠FEH}\\{AE=EF}\end{array}\right.$,
∴△ADE≌△EHF,
∴DE=FH=1,AD=EH,
∴EH=DC,
即DE+CE=CH+EC,
∴DE=CH=1,
在Rt△CFH中,FC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=4,n=60,那么机器人回到原点共走了24m.
小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=4,n=60,那么机器人回到原点共走了24m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com